题目内容
考查复合函数求导的基础知识以及导数知识的综合应用.
已知函数f(x)=ln(ax+1)+
,x≥0,其中a>0.
(1)若f(x)在x=1处取得极值,求a的值;
(2)若f(x)的最小值为1,求a的取值范围.
已知函数f(x)=ln(ax+1)+
| 1-x | 1+x |
(1)若f(x)在x=1处取得极值,求a的值;
(2)若f(x)的最小值为1,求a的取值范围.
分析:(1)求出f′(x),因为函数在x=1处取极值,所以f'(1)=0求出a即可;
(2)求出f′(x),再进行分类讨论:当a≥2时,f(x)在区间(0,+∞)上递增,f(x)的最小值为f(0)=1.
当0<a<2时,可确定f(x)的单调减区间,单调增区间从而可知,f(x)在x=
处取得最小值,不合,故可求a的取值范围.
(2)求出f′(x),再进行分类讨论:当a≥2时,f(x)在区间(0,+∞)上递增,f(x)的最小值为f(0)=1.
当0<a<2时,可确定f(x)的单调减区间,单调增区间从而可知,f(x)在x=
|
解答:解:(1)f′(x)=
-
=
.
因f(x)在x=1处取得极值,故f'(1)=0,解得a=1 (经检验).…(4分)
(2)f′(x)=
,因x≥0,a>0,故ax+1>0,1+x>0.
当a≥2时,在区间(0,+∞)上f'(x)≥0,f(x)递增,f(x)的最小值为f(0)=1.
当0<a<2时,由f'(x)>0,解得x>
;由f'(x)<0,解得x<
.
∴f(x)的单调减区间为(0,
),单调增区间为(
,+∞).
于是,f(x)在x=
处取得最小值f(
)<f(0)=1,不合.
综上可知,若f(x)得最小值为1,则a的取值范围是[2,+∞).…(10分)
注:不检验不扣分.
| a |
| ax+1 |
| 2 |
| (1+x)2 |
| ax2+a-2 |
| (ax+1)(1+x)2 |
因f(x)在x=1处取得极值,故f'(1)=0,解得a=1 (经检验).…(4分)
(2)f′(x)=
| ax2+a-2 |
| (ax+1)(1+x)2 |
当a≥2时,在区间(0,+∞)上f'(x)≥0,f(x)递增,f(x)的最小值为f(0)=1.
当0<a<2时,由f'(x)>0,解得x>
|
|
∴f(x)的单调减区间为(0,
|
|
于是,f(x)在x=
|
|
综上可知,若f(x)得最小值为1,则a的取值范围是[2,+∞).…(10分)
注:不检验不扣分.
点评:本题以函数为载体,考查学生利用导数研究函数极值的能力,考查复合函数求导的基础知识以及导数知识的综合应用,注意分类讨论思想的运用

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
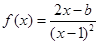 ,求导函数
,求导函数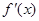 ,并确定
,并确定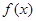 的单调区间
的单调区间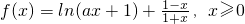 ,其中a>0.
,其中a>0.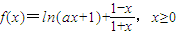 ,其中a>0.
,其中a>0.
