摘要： 下面给出了关于复数的四种类比推理: ①复数的加减法运算可以类比多项式的加减法运算法则, ②由向量a的性质|a|2=a2类比得到复数z的性质|z|2=z2, ③方程有两个不同实数根的条件是可以类比得到:方程有两个不同复数根的条件是, ④由向量加法的几何意义可以类比得到复数加法的几何意义. 其中类比错误的是 ( ) A.①③ B. ②④ C. ①④ D. ②③
网址：http://m.1010jiajiao.com/timu3_id_524003[举报]
下面给出了关于复数的四种类比推理：
①复数的加减法运算可以类比多项式的加减法运算法则；
②由向量a的性质|
|2=
2类比得到复数z的性质|z|2=z2；
③方程ax2+bx+c=0（a，b，c⊆R）有两个不同实数根的条件是b2-4ac＞0可以类比得到：方程az2+bz+c=0（a，b，c⊆C）有两个不同复数根的条件是b2-4ac＞0；
④由向量加法的几何意义可以类比得到复数加法的几何意义．
其中类比错误的是 ．
查看习题详情和答案>>
①复数的加减法运算可以类比多项式的加减法运算法则；
②由向量a的性质|
| a |
| a |
③方程ax2+bx+c=0（a，b，c⊆R）有两个不同实数根的条件是b2-4ac＞0可以类比得到：方程az2+bz+c=0（a，b，c⊆C）有两个不同复数根的条件是b2-4ac＞0；
④由向量加法的几何意义可以类比得到复数加法的几何意义．
其中类比错误的是
下面给出了关于复数的四种类比推理：
①复数的加减法运算可以类比多项式的加减法运算法则；
②由向量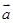
的性质
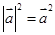类比得到复数
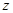的性质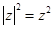
；
③方程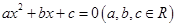
有两个不同实数根的条件是
可以类比得到：方程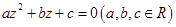
有两个不同复数根的条件是；
④由向量加法的几何意义可以类比得到复数加法的几何意义
其中类比得到的结论错误的是
| A．①③ | B．②④ | C．②③ | D．①④ |
下面给出了关于复数的四种类比推理：
①复数的加减法运算可以类比多项式的加减法运算法则；
②由向量
的性质
类比得到复数
的性质
；
③方程
有两个不同实数根的条件是
可以类比得到：方程
有两个不同复数根的条件是；
④由向量加法的几何意义可以类比得到复数加法的几何意义
其中类比得到的结论错误的是
A．①③ B．②④ C．②③ D．①④
查看习题详情和答案>>
的性质
，可以类比得到复数 
的性质
；
（a 、b 、c ∈ R ）有两个不同实根的条件是
,类比可以得到
方程 
（a 、b 、c ∈ C）有两个不同复数根的条件是
的性质 
，可以类比得到复数
的性质 
；
（a 、b 、c ∈ R ）有两个不同实根的条件是
, 类比可以得到 方程 
（a 、b 、c ∈ C）有两个不同复数根的条件是