摘要:(北师大版必修2第101页例8) 判断圆与圆的位置关系.并画出图形. 变式1:圆和圆的位置关系是( ) A.相离 B.外切 C.相交 D.内切 解:∵圆的圆心为.半径.圆的圆心为.半径.∴.∵.∴两圆相交.故选(C). 变式2:若圆与圆相切.则实数的取值集合是 . 解:∵圆的圆心为.半径.圆的圆心为.半径.且两圆相切.∴或.∴或.解得或.或或.∴实数的取值集合是. 变式3:求与圆外切于点.且半径为的圆的方程. 解:设所求圆的圆心为.则所求圆的方程为.∵两圆外切于点.∴.∴.∴.∴所求圆的方程为.
网址:http://m.1010jiajiao.com/timu3_id_523368[举报]
我们知道,判断直线与圆的位置关系可以用圆心到直线的距离进行判别,那么直线与椭圆的位置关系有类似的判别方法吗?请同学们进行研究并完成下面问题.
(1)设F1、F2是椭圆M:
+
=1的两个焦点,点F1、F2到直线L:
x-y+
=0的距离分别为d1、d2,试求d1•d2的值,并判断直线L与椭圆M的位置关系.
(2)设F1、F2是椭圆M:
+
=1(a>b>0)的两个焦点,点F1、F2到直线L:mx+ny+p=0(m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1•d2的值.
(3)试写出一个能判断直线与椭圆的位置关系的充要条件,并证明.
(4)将(3)中得出的结论类比到其它曲线,请同学们给出自己研究的有关结论(不必证明).
查看习题详情和答案>>
(1)设F1、F2是椭圆M:
| x2 |
| 25 |
| y2 |
| 9 |
| 2 |
| 5 |
(2)设F1、F2是椭圆M:
| x2 |
| a2 |
| y2 |
| b2 |
(3)试写出一个能判断直线与椭圆的位置关系的充要条件,并证明.
(4)将(3)中得出的结论类比到其它曲线,请同学们给出自己研究的有关结论(不必证明).
设抛物线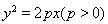 的焦点为
的焦点为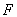 ,点
,点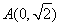 ,线段
,线段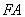 的中点在抛物线上.设动直线
的中点在抛物线上.设动直线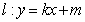 与抛物线相切于点
与抛物线相切于点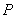 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点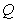 ,以
,以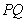 为直径的圆记为圆
为直径的圆记为圆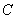 .
.
(1)求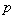 的值;
的值;
(2)试判断圆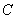 与
与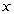 轴的位置关系;
轴的位置关系;
(3)在坐标平面上是否存在定点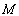 ,使得圆
,使得圆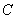 恒过点
恒过点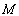 ?若存在,求出
?若存在,求出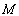 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看习题详情和答案>>
 上任取一点
上任取一点 ,过点
,过点 轴的垂线段
轴的垂线段 ,
, 为垂足.设
为垂足.设 为线段
为线段 上运动时,求点
上运动时,求点 的方程;
的方程; ,试判断直线
,试判断直线 与轨迹
与轨迹
 (II)设(I)中的直线
(II)设(I)中的直线 的焦点为
的焦点为 ,点
,点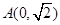 ,线段
,线段 的中点在抛物线上.设动直线
的中点在抛物线上.设动直线 与抛物线相切于点
与抛物线相切于点 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以 为直径的圆记为圆
为直径的圆记为圆 .
. 的值;
的值; 轴的位置关系;
轴的位置关系; ,使得圆
,使得圆