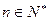摘要:20.已知数列中. (1)求证:数列与都是等比数列,(2)求数列前的和, (3)若数列前的和为.不等式对恒成立.求的最大值.
网址:http://m.1010jiajiao.com/timu3_id_523328[举报]
已知数列{an} 和 {bn}中,a1=t(t>0),a2=t2.当x=
时,函数f(x)=
(an-1-an)x3-(an-an+1)x(n≥2)取得极值.
(1)求数列{an} 的通项公式.
(2)若点Pn(1,bn).过函数g(x)=ln(1+x2)图象上的点(an,g(an))的切线始终与OPn平行(O是坐标原点).求证:当
<t<2时,不等式
+
+…+
<2n-2
对任意n∈N*都成立.
查看习题详情和答案>>
| t |
| 1 |
| 3 |
(1)求数列{an} 的通项公式.
(2)若点Pn(1,bn).过函数g(x)=ln(1+x2)图象上的点(an,g(an))的切线始终与OPn平行(O是坐标原点).求证:当
| 1 |
| 2 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| -n |
| 2 |
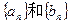 中,
中,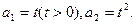 当
当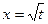 时,函数
时,函数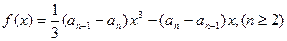 取得极值。
取得极值。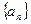 的通项公式。(6分)
的通项公式。(6分)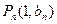 。过函数
。过函数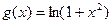 图象上的点
图象上的点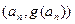 的切线始终与
的切线始终与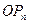 平行(O是坐标原点)。求证:当
平行(O是坐标原点)。求证:当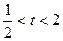 时,不等式
时,不等式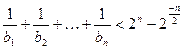 对任意
对任意