摘要：设 a,b,c是平面内任意的非零向量且相互不共线,则 ①(ab)c-(ca)b=0 ②|a| -|b|< |a-b| ③(bc)a-(ca)b不与c垂直 ④(3a+2b)(3a-2b)= 9|a|2-4|b|2 其中真命题是 ( ) A．①② B．②③ C．③④ D．②④
网址：http://m.1010jiajiao.com/timu3_id_523023[举报]
设a，b，c是平面内任意的非零向量且相互不共线，则
①(ab)c－(ca)b＝0
②|a|－|b|＜|a－b|
③(bc)a－(ca)b不与c垂直
④(3a＋2b)(3a－2b)＝9|a|2－4|b|2
其中真命题是
[ ]
A．
①②
B．
②③
C．
③④
D．
②④
有下列几个命题：①若
与
都是非零向量，则“
”是“
”的充要条件；②已知等腰△ABC的腰为底的2倍，则顶角A的正切值是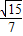
；③在平面直角坐标系xoy中，四边形ABCD的边AB∥DC，AD∥BC，已知点A（-2，0），B（6，8），C（8，6），则D点的坐标为（0，-1）；④设
，
，
为同一平面内具有相同起点的任意三个非零向量，且满足
与
不共线，
⊥
，|
|=|
|，则|
•
|的值一定等于以
，
为邻边的平行四边形的面积．其中正确命题的序号是 ．（写出全部正确结论的序号）
查看习题详情和答案>>
与都是非零向量，则“”是“”的充要条件；②已知等腰△ABC的腰为底的2倍，则顶角A的正切值是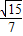；③在平面直角坐标系xoy中，四边形ABCD的边AB∥DC，AD∥BC，已知点A（-2，0），B（6，8），C（8，6），则D点的坐标为（0，-1）；④设，，为同一平面内具有相同起点的任意三个非零向量，且满足与不共线，⊥，||=||，则|•|的值一定等于以，为邻边的平行四边形的面积．其中正确命题的序号是 ．（写出全部正确结论的序号）
查看习题详情和答案>>