摘要:利用向量的数量积解决线与线的夹角及面与面的夹角问题. [例9] 证明: 证明:在单位圆上任取两点.以为始边.以为终边的角分别为.则点坐标为点坐标为, 则向量.它们的夹角为. ,由向量夹角公式得: ,从而得证. 注:用同样的方法可证明
网址:http://m.1010jiajiao.com/timu3_id_523013[举报]
在 中,满足
中,满足 ,
, 是
是 边上的一点.
边上的一点.
(Ⅰ)若 ,求向量
,求向量 与向量
与向量 夹角的正弦值;
夹角的正弦值;
(Ⅱ)若 ,
, =m (m为正常数) 且
=m (m为正常数) 且 是
是 边上的三等分点.,求
边上的三等分点.,求 值;
值;
(Ⅲ)若 且
且 求
求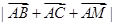 的最小值。
的最小值。
【解析】第一问中,利用向量的数量积设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则 为所求
为所求
第二问因为 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则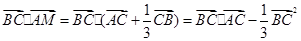 =
=
(2)当 时,则
时,则 =
=
第三问中,解:设 ,因为
,因为
 ,
, ;
;
所以 即
即 于是
于是 得
得
从而
运用三角函数求解。
(Ⅰ)解:设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则 为所求……………2分
为所求……………2分
(Ⅱ)解:因为 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则 =
= ;-2分
;-2分
(2)当 时,则
时,则 =
= ;--2分
;--2分
(Ⅲ)解:设 ,因为
,因为
 ,
, ;
;
所以 即
即 于是
于是 得
得
从而 ---2分
---2分
= =
=
= …………………………………2分
…………………………………2分
令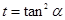 ,
, 则
则 ,则函数
,则函数 ,在
,在 递减,在
递减,在 上递增,所以
上递增,所以 从而当
从而当 时,
时,
查看习题详情和答案>>
设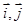 是直角坐标系中,x轴、y轴正方向上的单位向量,设
是直角坐标系中,x轴、y轴正方向上的单位向量,设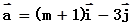
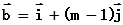
(1)若(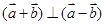 ,求
,求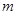 .
.
(2)若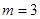 时,求
时,求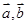 的夹角
的夹角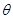 的余弦值.
的余弦值.
(3)是否存在实数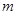 ,使
,使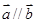 ,若存在求出
,若存在求出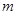 的值,不存在说明理由.
的值,不存在说明理由.
【解析】第一问中,利用向量的数量积为0,解得为m=-2
第二问中,利用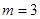 时,结合向量
时,结合向量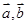 的夹角
的夹角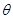 的余弦值公式解得
的余弦值公式解得
第三问中,利用向量共线,求解得到m不存在。
(1)因为设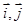 是直角坐标系中,x轴、y轴正方向上的单位向量,设
是直角坐标系中,x轴、y轴正方向上的单位向量,设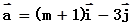
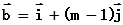
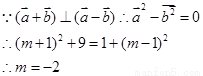
(2)因為
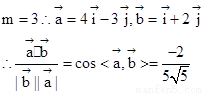
即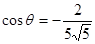 ;
;
(3)假設存在实数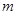 ,使
,使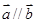 ,則有
,則有
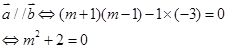
因此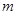 不存在;
不存在;
查看习题详情和答案>>

 ;
; 在向量
在向量 方向上的投影.
方向上的投影.

 ,然后利用投影的定义得到向量
,然后利用投影的定义得到向量 =
=


 ,试判断b·c取得最大值时△ABC形状.
,试判断b·c取得最大值时△ABC形状. ,且由
,且由
 ,以及
,以及 ,可知
,可知 ,并为等边三角形。
,并为等边三角形。
 ………………………………6分
………………………………6分 ………………………………8分
………………………………8分