在平面上.设ha.hb.hc是三角形ABC三条边上的高．P为三角形内任一点.P到相应三边的距离分别为pa.pb.pc.我们可以得到结论:paha+pbhb+pchc=1试通过类比.写出在空间中的类似结论题目和参考答案——青夏教育精英家教网—

题目内容

在平面上，设h_a，h_b，h_c是三角形ABC三条边上的高．P为三角形内任一点，P到相应三边的距离分别为p_a，p_b，p_c，我们可以得到结论：

=1试通过类比，写出在空间中的类似结论

分析：本题是一道有关三角形与三棱锥的归纳类比题，这类题的特点是：往往并不需要证明结论，主要考查考生的创新精神，是否会观察，会抽象概括，会用类比的方法得出新的一般性的结论．这类题目经常出现在高考试题中，经常以数列或解析几何或立体几何等知识为载体．

解答：解：设h_a，h_b，h_c，h_d三棱锥A-BCD四个面上的高．
P为三棱锥A-BCD内任一点，
P到相应四个面的距离分别为p_a，p_b，p_c，p_d我们可以得到结论：

=1．
V_P-ABC+V_P-BCD+V_P-CDA+V_P-DAB=V，V=V_D-ABC=V_A-BCD=V_B-CDA=V_C-DAB，
即

VP-ABC

VD-ABC

VP-BCD

VA-BCD

VP-CDA

VB-CDA

VP-DAB

VC-DAB

=1，

SABC•pd

SABC•hd

SBCD•pa

SBCD•ha

SCDA•pb

SCDA•hb

SDAB•pc

SDABhc

=1，
即

=1．
故答案为：

=1．

点评：类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．

练习册系列答案

高中新课标同步用书全优课堂系列答案

实验探究报告册系列答案

金版学案高中同步辅导与检测系列答案

名师金典高中新课标同步攻略与测评系列答案

相关题目

在(0，+∞)是减函数；
②在平面上，到定点（2，-1）的距离与到定直线3x-4y-10=0距离相等的点的轨迹是抛物线；
③设函数f(x)=cos(

)，则f（x）+f'（x）是奇函数；
④双曲线

=1的一个焦点到渐近线的距离是5；
其中正确命题的序号是

③

．

类比平面上的命题（m），给出在空间中的类似命题（n）的猜想．
（m）如果△ABC的三条边BC，CA，AB上的高分别为h_a，h_b和h_c，△ABC内任意一点P到三条边BC，CA，AB的距离分别为P_a，P_b，P_c，那么

=1．
（n）

设h_a，h_b，h_c，h_d为四面体S-ABC的四个面上的高，P为四面体内的任一点，
P到相应四个面的距离分别为P_a，P_b，P_c，p_d，那么

．

在平面上，设h_a，h_b，h_c是三角形ABC三条边上的高．P为三角形内任一点，P到相应三边的距离分别为p_a，p_b，p_c，我们可以得到结论：

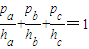试通过类比，写出在空间中的类似结论

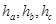在平面上,设是三角形ABC三条边上的高.P为三角形内任一点,P到相应三边的距离分别为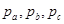,我们可以得到结论: 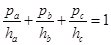类比到空间中的四面体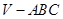内任一点p, 其中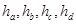为四面体四个面上的高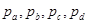，为p点到四个面的距离，我们可以得到类似结论为

试题分类