摘要:定义在上的任意函数f(x)都可以表示成一个奇函数g(x)和一个偶函数h(x)之和.如果f(x)=lg(10x+1),其中x∈ A.g(x)=x,h(x)=lg(10x+10-x+2) B.g(x)=[lg(10x+1)+x],h(x)= [lg(10x+1)-x] C.g(x)=,h(x)=lg(10x+1)- D.g(x)=-,h(x)=lg(10x+1)+
网址:http://m.1010jiajiao.com/timu3_id_522987[举报]
定义在(-∞,+∞)上的任意函数f(x)都可以表示成一个奇函数g(x)和一个偶函数h(x)之和,如果f(x)=lg(10x+1),其中x∈(-∞,+∞),那么( )
A. g(x)=x,h(x)=lg(10x+10-x+2)
B. g(x)=![]() [lg(10x+1)+x],h(x)=
[lg(10x+1)+x],h(x)= ![]() [lg(10x+1)-x]
[lg(10x+1)-x]
C. g(x)=![]() ,h(x)=lg(10x+1)-
,h(x)=lg(10x+1)-![]()
D. g(x)=-![]() ,h(x)=lg(10x+1)+
,h(x)=lg(10x+1)+![]()
定义在R上的任意函数f (x)都可以表示成一个奇函数g (x)和一个偶函数h (x)之和,如果f (x)=lg(10x+1),x∈R.那么
A.g (x)=x,h (x)=lg(10x+10-x+1)
B.g (x)= ,h (x)=
,h (x)=
C.g (x)= ,h (x)=lg(10x+1)-
,h (x)=lg(10x+1)-
D.g (x)=- ,h (x)=
,h (x)=
查看习题详情和答案>>
定义在R上的任意函数f (x)都可以表示成一个奇函数g (x)和一个偶函数h (x)之和,如果f (x)=lg(10x+1),x∈R.那么
| A.g (x)=x,h (x)=lg(10x+10-x+1) |
B.g (x)= ,h (x)= ,h (x)= |
C.g (x)= ,h (x)=lg(10x+1)- ,h (x)=lg(10x+1)- |
D.g (x)=- ,h (x)= ,h (x)= |
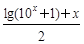 ,h (x)=
,h (x)=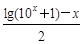
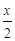 ,h (x)=lg(10x+1)-
,h (x)=lg(10x+1)-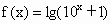 ,xÎ(-¥,+¥),求g(x)和h(x).
,xÎ(-¥,+¥),求g(x)和h(x).