摘要:已知数列的通项公式为.求前项的和,(2)已知数列的通项公式为.求前项的和. 变式题1.已知数列的通项公式为=.设.求. 解:==2(-). =2[(-)+(-)+(-)+--+(-)+(-)]=2(+--). 变式题2.数列{an}中.a1=8.a4=2.且满足:an+2-2an+1+an=0. (Ⅰ)求数列{an}的通项公式, (Ⅱ)设.是否存在最大的整数m.使得任意的n均有总成立?若存在.求出m,若不存在.请说明理由. 解:(Ⅰ)∵an+2-2an+1+an=0.∴an+2-an+1=an+1-an. ∴{an}是等差数列.设公差为d. ∵a1=8.a4=a1+3d=8+3d=2.∴d=-2. ∴an=8+(n-1)·(-2)=10-2n. (Ⅱ) 假设存在整数m满足总成立. 又 ∴数列{}是单调递增的. ∴为的最小值.故.即m<8.又m∈N*. ∴适当条件的m的最大值为7. 点评:数列求和的裂项相消法:适用于通项公式形如的数列.其中是各项不为0的等差数列.c为常数.
网址:http://m.1010jiajiao.com/timu3_id_522970[举报]
 ,则前n项的和 ________;(2)已知数列an的通项公式为
,则前n项的和 ________;(2)已知数列an的通项公式为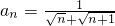 ,则前n项的和 ________.
,则前n项的和 ________. ,则前n项的和 ;(2)已知数列an的通项公式为
,则前n项的和 ;(2)已知数列an的通项公式为 ,则前n项的和 .
,则前n项的和 .