摘要：设数列{an}的前n项和为Sn.且Sn=(m+1)-man.对任意正整数n都成立.其中m为常数.且m＜-1. (1)求证:{an}是等比数列, (2)设数列{an}的公比q=f(m).数列{bn}满足:b1=a1,bn=f(bn-1)(n≥2,n∈N*).试问当m为何值时.成立?
网址：http://m.1010jiajiao.com/timu3_id_522958[举报]
设数列{an}的前n项和为Sn，且Sn=(m+1)－man
对任意正整数n都成立，其中m为常数，且m＜－1.
(1)求证:{an}是等比数列；
(2)设数列{an}的公比q=f(m)，数列{bn}满足:b1=
a1,bn=f(bn－1)(n≥2,n∈N*). 试问当m为何值时，
成立？
设数列{an}的前n项和为Sn，且Sn=(m+1)－man
对任意正整数n都成立，其中m为常数，且m＜－1.
(1)求证:{an}是等比数列；
(2)设数列{an}的公比q=f(m)，数列{bn}满足:b1=
a1,bn=f(bn－1)(n≥2,n∈N*). 试问当m为何值时，
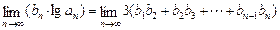成立？
对任意正整数n都成立，其中m为常数，且m＜－1.(1)求证:{an}是等比数列；
(2)设数列{an}的公比q=f(m)，数列{bn}满足:b1=
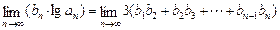a1,bn=f(bn－1)(n≥2,n∈N*). 试问当m为何值时，成立？设数列{an}的前n项和为Sn，且Sn=9n-n2．
（1）求数列{an}的通项公式；
（2）设bn=
（n∈N+），数列{bn}的前n项和为Tn，若对任意的n∈N+，均有Tn＞
，求m的取值范围．
查看习题详情和答案>>
（1）求数列{an}的通项公式；
（2）设bn=
| 1 |
| n(12-an) |
| m2-3m+7 |
| 20 |