摘要: 设P点是椭圆上异于长轴端点的任一点,F1.F2为其焦点记.则(1).(2) .
网址:http://m.1010jiajiao.com/timu3_id_522828[举报]
设椭圆
+
=1(a>b>0)的两个焦点是F1和F2,长轴是A1A2,P是椭圆上异于A1、A2的点,考虑如下四个命题:
①|PF1|-|A1F1|=|A1F2|-|PF2|;
②a-c<|PF1|<a+c;
③若b越接近于a,则离心率越接近于1;
④直线PA1与PA2的斜率之积等于-
.
其中正确的命题是( )
| x2 |
| a2 |
| y2 |
| b2 |
①|PF1|-|A1F1|=|A1F2|-|PF2|;
②a-c<|PF1|<a+c;
③若b越接近于a,则离心率越接近于1;
④直线PA1与PA2的斜率之积等于-
| b2 |
| a2 |
其中正确的命题是( )
| A、①②④ | B、①②③ |
| C、②③④ | D、①④ |
设椭圆
+
=1(a>b>0)的两个焦点是F1和F2,长轴是A1A2,P是椭圆上异于A1、A2的点,考虑如下四个命题:
①|PF1|-|A1F1|=|A1F2|-|PF2|;
②a-c<|PF1|<a+c;
③若b越接近于a,则离心率越接近于1;
④直线PA1与PA2的斜率之积等于-
.
其中正确的命题是( )
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
①|PF1|-|A1F1|=|A1F2|-|PF2|;
②a-c<|PF1|<a+c;
③若b越接近于a,则离心率越接近于1;
④直线PA1与PA2的斜率之积等于-
| b2 |
| a2 |
其中正确的命题是( )
| A.①②④ | B.①②③ | C.②③④ | D.①④ |
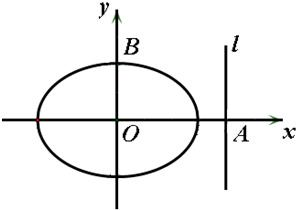 已知椭圆E:
已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
4
| ||
| 5 |
(1)求椭圆E的方程及圆O的方程;
(2)若M是准线l上纵坐标为t的点,求证:存在一个异于M的点Q,对于圆O上任意一点N,有
| MN |
| NQ |
 已知椭圆E:
已知椭圆E: