摘要: AB是椭圆的不平行于对称轴的弦.M为AB的中点.则. 即.
网址:http://m.1010jiajiao.com/timu3_id_522802[举报]
与圆类似,连接圆锥曲线上两点的线段叫做圆锥曲线的弦.过有心曲线(椭圆、双曲线)中心(即对称中心)的弦叫做有心曲线的直径.对圆x2+y2=r2,由直径所对的圆周角是直角出发,可得:若AB是圆O的直径,M是圆O上异于A、B的一点,且AM,BM均与坐标轴不平行,则kAM•kBM=-1.类比到椭圆
+
=1,类似结论是
.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
若AB是椭圆
+
=1的直径,M是椭圆上异于A、B的一点,且AM、BM均与坐标轴不平行,则kAM•kBM=-
.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
若AB是椭圆
+
=1的直径,M是椭圆上异于A、B的一点,且AM、BM均与坐标轴不平行,则kAM•kBM=-
.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
.
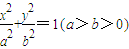 中不平行于对称轴的一条弦,M是AB的中点,O是椭圆的中心,求证:kAB•kOM为定值.
中不平行于对称轴的一条弦,M是AB的中点,O是椭圆的中心,求证:kAB•kOM为定值.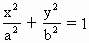 (a>b>0)中不平行于对称轴且不过原点O的一条弦,M是AB的中点,求证:
(a>b>0)中不平行于对称轴且不过原点O的一条弦,M是AB的中点,求证: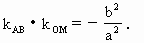
 ,类似结论是________
,类似结论是________