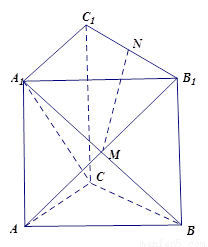
摘要:18. 如图.三棱柱ABC-A1B1C1中.AA1⊥面ABC.BC⊥AC.BC=AC=2.AA1=3.D为AC的中点. (Ⅰ)求证:AB1//面BDC1, (Ⅱ)求二面角C1-BD-C的余弦值, (Ⅲ)在侧棱AA1上是否存在点P.使得 CP⊥面BDC1?并证明你的结论.
网址:http://m.1010jiajiao.com/timu3_id_522780[举报]
(本小题满分14分)如图,在直三棱柱ABC—A1B1C1中,AB=AC,点D是BC的中点.

(1)求证:A1B//平面ADC1;
(2)如果点E是B1C1的中点,求证:平面 平面BCC1B1.
平面BCC1B1.
查看习题详情和答案>>
(本小题满分14分)如图,在直三棱柱ABC—A1B1C1中,![]() ,
,![]() ,
,![]() ,
,![]() ,点D在棱
,点D在棱![]() 上,且
上,且![]() ∶
∶![]() ∶3 w.
∶3 w. ![]()
![]() (1)证明:无论a为任何正数,均有BD⊥A1C;
(1)证明:无论a为任何正数,均有BD⊥A1C;
(2)当a为何值时,二面角B—A1D—B1为60°?
查看习题详情和答案>>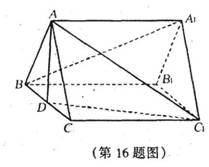 (2)A1B∥平面ADC1.
(2)A1B∥平面ADC1.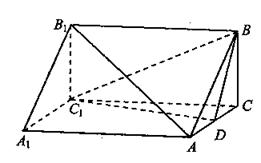
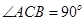 ,M为A1B与AB1的交点,N为棱B1C1的中点
,M为A1B与AB1的交点,N为棱B1C1的中点