摘要:9.(北师大版第144页A组第1题)三角函数的简单应用 电流I随时间t 变化的关系式..设 .. (1) 求电流I变化的周期, (2) 当(单位)时.求电流I. 变式1:已知电流I与时间t的关系式为. (1)右图是(ω>0.) 在一个周期内的图象.根据图中数据求的解析式, (2)如果t在任意一段秒的时间内.电流都能取得最大值和最小值.那么ω的最小正整数值是多少? 解:(1)由图可知 A=300. 设t1=-.t2=. 则周期T=2(t2-t1)=2(+)=. ∴ ω==150π. 又当t=时.I=0.即sin(150π·+)=0. 而. ∴ =. 故所求的解析式为. (2)依题意.周期T≤.即≤.(ω>0) ∴ ω≥300π>942.又ω∈N*. 故最小正整数ω=943. 变式2:如图.某地一天从6时至14时的温度变化曲线近似 满足函数y=Asin(ωx+)+b. (Ⅰ)求这段时间的最大温差, (Ⅱ)写出这段曲线的函数解析式. 解:(1)由题中图所示.这段时间的最大温差是: 30-10=20(℃). (2)图中从6时到14时的图象是函数y=Asin(ωx+)+b的半个周期的图象. ∴·=14-6.解得ω=. 由图示.A==10.b==20. 这时y=10sin(x+)+20. 将x=6.y=10代入上式.可取=. 综上.所求的解析式为y=10sin(x+)+20.x∈[6.14] 变式3:如图.单摆从某点给一个作用力后开始来回摆动. 离开平衡位置O的距离s厘米和时间t秒的函数关系 为. (1)单摆摆动5秒时.离开平衡位置多少厘米? (2)单摆摆动时.从最右边到最左边的距离为多少厘米? (3)单摆来回摆动10次所需的时间为多少秒?
网址:http://m.1010jiajiao.com/timu3_id_521821[举报]
在函数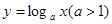 的图象上有
的图象上有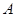 、
、 、
、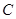 三点,横坐标分别为
三点,横坐标分别为 其中
其中 .
.
⑴求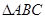 的面积
的面积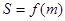 的表达式;
的表达式;
⑵求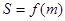 的值域.
的值域.
【解析】由题意利用分割可先表示三角形ABC的面积,然后应用对数运算性质及二次函数的性质求解函数的最大值,属于知识的简单综合.
查看习题详情和答案>>
有四个关于三角函数的命题:p1:存在x∈R,使得sin2
+cos2
=
;p2:若一个三角形两内角α、β满足sinα•cosβ<0,则此三角形为钝角三角形;p3:任意的x∈[0,π],都有sinx=
;p4:要得到函数y=sin(
-
)的图象,只需将函数y=sin
的图象向右平移
个单位.其中假命题的是( )
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
|
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
查看习题详情和答案>>
有四个关于三角函数的命题:
P1:?x∈R,sin2
+cos2
=
;
P2:?x、y∈R,sin(x-y)=sinx-siny;
P3:?x∈[0,π],
=sinx;
P4:sinx=cosy?x+y=
.
其中假命题的是( )
P1:?x∈R,sin2
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
P2:?x、y∈R,sin(x-y)=sinx-siny;
P3:?x∈[0,π],
|
P4:sinx=cosy?x+y=
| π |
| 2 |
其中假命题的是( )
| A、P1,P4 |
| B、P2,P4 |
| C、P1,P3 |
| D、P2,P4 |