摘要:22.解: (Ⅰ)由于则P为MN的中心.--1分. 设N(x.y).则M(-x,0),P(0.).--.由得 所以点N的轨迹方程为--5分 (Ⅱ)设直线l的方程是 与: --------6分 设则: --------7分 由 即 ----9分 由于直线与N的轨迹交于不同的两点.则 把 ------10分 而 -11分 又因为 解得 综上可知k的取值范围是.-14分
网址:http://m.1010jiajiao.com/timu3_id_520876[举报]
已知抛物线y2=4ax(a>0)的焦点为F,以点A(a+4,0)为圆心,|AF|为半径的圆在x轴的上方与抛物线交于M、N两点.
(I)求证:点A在以M、N为焦点,且过点F的椭圆上;
(II)设点P为MN的中点,是否存在这样的a,使得|FP|是|FM|与|FN|的等差中项?如果存在,求出实数a的值;如果不存在,请说明理由. 查看习题详情和答案>>
(I)求证:点A在以M、N为焦点,且过点F的椭圆上;
(II)设点P为MN的中点,是否存在这样的a,使得|FP|是|FM|与|FN|的等差中项?如果存在,求出实数a的值;如果不存在,请说明理由. 查看习题详情和答案>>
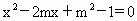 的两根均大于-2小于4,则p为q的
的两根均大于-2小于4,则p为q的