摘要：23．如图.直线相交于点P.直线l1与x轴交于点P1.过点P1作x轴的垂线交直线l2于点Q1.过点Q1作y轴的垂线交直线l1于点P2.过点P2作x轴的垂线交直线l2于点Q2.-.这样一直作下去.可得到一系列点P1.Q1.P2.Q2.-.点Pn的横坐标构成数列 (Ⅰ)证明, (Ⅱ)求数列的通项公式, (Ⅲ)比较的大小. (Ⅰ)证明:设点Pn的坐标是.由已知条件得 点Qn.Pn+1的坐标分别是: 由Pn+1在直线l1上.得 所以 即 (Ⅱ)解:由题设知 又由(Ⅰ)知 . 所以数列 是首项为公比为的等比数列. 从而 (Ⅲ)解:由得点P的坐标为(1.1). 所以 (i)当时.>1+9=10. 而此时 (ii)当时.<1+9=10. 而此时
网址：http://m.1010jiajiao.com/timu3_id_520599[举报]
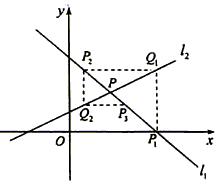
如图，直线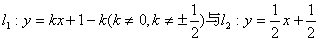
相交于点P.直线l1与x轴交于点P1，过点P1作x轴的垂线交直线l2于点Q1，过点Q1作y轴的垂线交直线l1于点P2，过点P2作x轴的垂线交直线l2于点Q2，…，这样一直作下去，可得到一系列点P1、Q1、P2、Q2，…，点Pn（n=1，2，…）的横坐标构成数列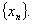
相交于点P.直线l1与x轴交于点P1，过点P1作x轴的垂线交直线l2于点Q1，过点Q1作y轴的垂线交直线l1于点P2，过点P2作x轴的垂线交直线l2于点Q2，…，这样一直作下去，可得到一系列点P1、Q1、P2、Q2，…，点Pn（n=1，2，…）的横坐标构成数列
（Ⅰ）证明
；
（Ⅱ）求数列
的通项公式；
（Ⅲ）比较
的大小.
查看习题详情和答案>>
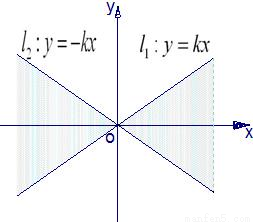
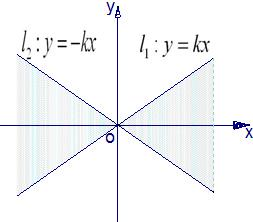如图，直线l1：y=kx（k＞0）与直线l2：y=-kx之间的阴影区域（不含边界）记为W，其左半部分记为W1，右半部分记为W2．（Ⅰ）分别用不等式组表示W1和W2．
（Ⅱ）若区域W中的动点P（x，y）到l1，l2的距离之积等于d2，求点P的轨迹C的方程；
（Ⅲ）设不过原点O的直线l与（Ⅱ）中的曲线C相交于M1，M2两点，且与l1，l2分别交于M3，M4两点．求证△OM1M2的重心与△OM3M4的重心重合． 查看习题详情和答案>>
如图，直线l1：y=kx（k＞0）与直线l2：y=-kx之间的阴影区域（不含边界）记为W，其左半部分记为W1，右半部分记为W2，
（Ⅰ）分别用不等式组表示W1和W2；
（Ⅱ）若区域W中的动点P（x，y）到l1，l2的距离之积等于d2，求点P的轨迹C的方程；
（Ⅲ）设不过原点O的直线l与（Ⅱ）中的曲线C相交于M1，M2两点，且与l1，l2分别交于M3，M4两点，求证△OM1M2的重心与△OM3M4的重心重合。
（Ⅰ）分别用不等式组表示W1和W2；
（Ⅱ）若区域W中的动点P（x，y）到l1，l2的距离之积等于d2，求点P的轨迹C的方程；
（Ⅲ）设不过原点O的直线l与（Ⅱ）中的曲线C相交于M1，M2两点，且与l1，l2分别交于M3，M4两点，求证△OM1M2的重心与△OM3M4的重心重合。
