摘要:18. 解:由图可知.参加活动1次.2次和3次的学生人数分别为10.50和40. (I)该合唱团学生参加活动的人均次数为. (II)从合唱团中任选两名学生.他们参加活动次数恰好相等的概率为. (III)从合唱团中任选两名学生.记“这两人中一人参加1次活动.另一人参加2次活动 为事件.“这两人中一人参加2次活动.另一人参加3次活动 为事件.“这两人中一人参加1次活动.另一人参加3次活动 为事件.易知 , , 的分布列: 0 1 2 的数学期望:.
网址:http://m.1010jiajiao.com/timu3_id_520303[举报]
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
现有5名同学的物理和数学成绩如下表:
| 物理 | 64 | 61 | 78 | 65 | 71 |
| 数学 | 66 | 63 | 88 | 76 | 73 |
(1)画出散点图;
(2)若![]() 与
与![]() 具有线性相关关系,试求变量
具有线性相关关系,试求变量![]() 对
对![]() 的回归方程并求变量
的回归方程并求变量![]() 对
对![]() 的回归方程.
的回归方程.
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
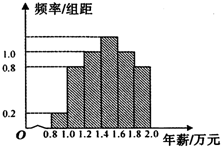 某公司300名员工2012年年薪情况的频率分布直方图如图所示,由图可知,员工中年薪在1.4-1.6万元的共有
某公司300名员工2012年年薪情况的频率分布直方图如图所示,由图可知,员工中年薪在1.4-1.6万元的共有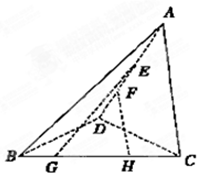 如图,E?F是AD上互异的两点,G?H是BC上互异的两点,由图可知,①AB与CD互为异面直线;②FH分别与DC?DB互为异面直线;③EG与FH互为异面直线;④EG与AB互为异面直线.其中叙述正确的是( )
如图,E?F是AD上互异的两点,G?H是BC上互异的两点,由图可知,①AB与CD互为异面直线;②FH分别与DC?DB互为异面直线;③EG与FH互为异面直线;④EG与AB互为异面直线.其中叙述正确的是( )