摘要:18.解:(1)记表示事件“取出的2件产品中无二等品 . 表示事件“取出的2件产品中恰有1件二等品 . 则互斥.且.故 于是. 解得. (2)的可能取值为. 若该批产品共100件.由(1)知其二等品有件.故 . . . 所以的分布列为 0 1 2 全国II文
网址:http://m.1010jiajiao.com/timu3_id_520261[举报]
甲袋内装有2个红球和3个白球,乙袋内装有1个红球和n(n∈N*)个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为f(n).则以下关于函数f(n)(n∈N*)的判断正确的是( )
甲袋内装有2个红球和3个白球,乙袋内装有1个红球和
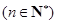 个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为
个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为 .则以下关于函数
.则以下关于函数
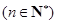 的判断正确的是
的判断正确的是
A. 有最小值,且最小值为 有最小值,且最小值为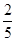 | B. 有最大值,且最大值为 有最大值,且最大值为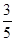 |
C. 有最小值,且最小值为 有最小值,且最小值为 | D. 有最大值,且最大值为 有最大值,且最大值为 |
甲袋内装有2个红球和3个白球,乙袋内装有1个红球和
 个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为
个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为 .则以下关于函数
.则以下关于函数
 的判断正确的是
的判断正确的是
A. 有最小值,且最小值为
有最小值,且最小值为 B.
B. 有最大值,且最大值为
有最大值,且最大值为
C. 有最小值,且最小值为
有最小值,且最小值为 D.
D. 有最大值,且最大值为
有最大值,且最大值为
查看习题详情和答案>>