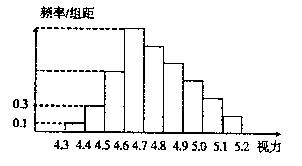
摘要：如右图所示.已知AB是平面α的 一条斜线.为平面α的法向量.则 C B A到平面α的距离为 α 例3.已知ABCD是边长为4的正方形.E.F分别是AB.AD的中点.GC垂直于ABCD所在的平面.且GC=2.求点B到平面EFG的距离. 分析:建立如图所示右手直角坐标系. G 则E. E D C G. A F B =.=.=.设平面EFG的法向量=.则由.得 -4x+2y+2z=0 x= -2x+4y+2z=0 y= 不妨设z=3.则=,所以依公式可得所求距离为
网址：http://m.1010jiajiao.com/timu3_id_520237[举报]
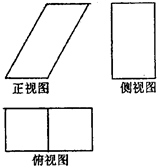一个几何体的三视图如右图所示．已知正视图是底边长为1的平行四边形，侧视图是一个长为| 3 |
（Ⅰ）求该几何体的体积V；
（Ⅱ）求该几何体的表面积S． 查看习题详情和答案>>
一个几何体的三视图如右图所示．已知正视图是底边长为1的平行四边形，侧视图是一个长为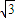
，宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．
（Ⅰ）求该几何体的体积V；
（Ⅱ）求该几何体的表面积S．
查看习题详情和答案>>
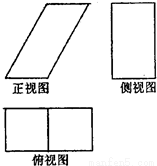
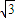，宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．（Ⅰ）求该几何体的体积V；
（Ⅱ）求该几何体的表面积S．
查看习题详情和答案>>
如右图所示，已知△OAB中，点C是以A为中心的点B的对称点，D在OB上，且| OD |
| DB |
| OA |
| a |
| OB |
| b |
（1）用
| a |
| b |
| OC |
| DC |
（2）若
| OE |
| OA |
（2011•延安模拟）如右图所示，已知0为矩形ABCD的边CD上一点，以直线CD为旋转轴，旋转这个矩形所得的几何体体积为1，其中以OA为母线的圆锥体积为