摘要:42.(天津•理•19题)如图.在四棱锥中.底面...是的中点. (Ⅰ)证明, (Ⅱ)证明平面, (Ⅲ)求二面角的大小, 分析:本小题考查直线与直线垂直.直线与平面垂直.二面角等基础知识.考查空间想象能力.运算能力和推理论证能力.满分12分. 解答:(Ⅰ)证明:在四棱锥中.因底面.平面.故. .平面. 而平面.. (Ⅱ)证明:由..可得. 是的中点.. 由(Ⅰ)知..且.所以平面. 而平面.. 底面在底面内的射影是... 又.综上得平面. (Ⅲ)解法一:过点作.垂足为.连结.则(Ⅱ)知.平面.在平面内的射影是.则. 因此是二面角的平面角. 由已知.得.设. 可得. 在中... 则.在中.. 所以二面角的大小是. 解法二:由题设底面.平面.则平面平面.交线为. 过点作.垂足为.故平面.过点作.垂足为.连结.故.因此是二面角的平面角. 由已知.可得.设. 可得. .. 于是.. 在中.. 所以二面角的大小是.
网址:http://m.1010jiajiao.com/timu3_id_520195[举报]
(2009江西卷文)(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() .以
.以![]() 的中点
的中点![]() 为球心、
为球心、![]() 为直径的球面交
为直径的球面交![]() 于点
于点![]() .
.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角;
所成的角;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.

查看习题详情和答案>>
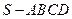 中,底面
中,底面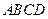 是正方形,
是正方形,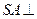 底面
底面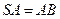 , 点
, 点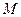 是
是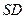 的中点,
的中点,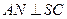 ,且交
,且交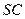 于点
于点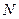 .
.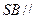 平面
平面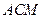 ;
;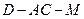 的余弦值大小;
的余弦值大小;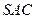 ⊥平面
⊥平面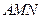 .
.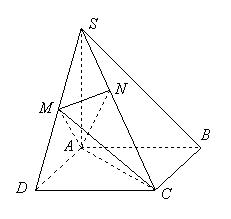
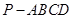 中,
中,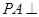 底面
底面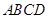 ,
,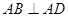 ,
,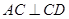 ,
,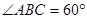 ,
,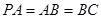 .
.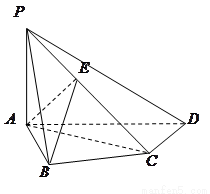
 平面
平面 ;
;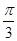 ,并说明理由.
,并说明理由.
 中,底面
中,底面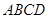 是正方形,侧棱
是正方形,侧棱 =2,
=2, ,垂足为F。
,垂足为F。