摘要:34.(湖南•理•18题)如图1.分别是矩形的边的中点.是上的一点.将.分别沿翻折成..并连结.使得平面平面..且.连结.如图2. (I)证明:平面平面, (II)当..时.求直线和平面所成的角, 解:解法一:(I)因为平面平面.平面平面..平面.所以平面.又平面.所以平面平面. (II)过点作于点.连结. 由(I)的结论可知.平面. 所以是和平面所成的角. 因为平面平面.平面平面.. 平面.所以平面.故. 因为..所以可在上取一点.使.又因为.所以四边形是矩形. 由题设...则.所以.. .. 因为平面..所以平面.从而. 故.. 又.由得. 故. 即直线与平面所成的角是. 解法二:(I)因为平面平面.平面平面.. 平面.所以平面.从而.又.所以平面.因为平面.所以平面平面. 可知.平面.故可以为原点.分别以直线为轴.轴.轴建立空间直角坐标系. 由题设...则. ..相关各点的坐标分别是. ... 所以.. 设是平面的一个法向量. 由得故可取. 过点作平面于点.因为.所以.于是点在轴上. 因为.所以.. 设().由.解得. 所以. 设和平面所成的角是.则 . 故直线与平面所成的角是.
网址:http://m.1010jiajiao.com/timu3_id_520187[举报]
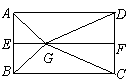
如图1,![]() 分别是矩形
分别是矩形![]() 的边
的边![]() 的中点,
的中点,![]() 是
是![]() 上的一点,将
上的一点,将![]() ,
,![]() 分别沿
分别沿![]() 翻折成
翻折成![]() ,
,![]() ,并连结
,并连结![]() ,使得平面
,使得平面![]() 平面
平面![]() ,
,![]() ,且
,且![]() .连结
.连结![]() ,如图2.
,如图2.
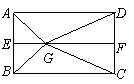
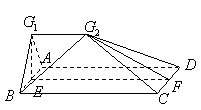
图1 图2
(I)证明:平面![]() 平面
平面![]() ;
;
(II)当![]() ,
,![]() ,
,![]() 时,求直线
时,求直线![]() 和平面
和平面![]() 所成的角.
所成的角.
 与圆
与圆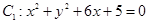 外切,同时与圆
外切,同时与圆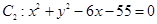 内切.
内切.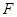 的方程;
的方程; 中(如图),
中(如图),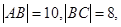
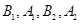 分别是矩形四边的中点,
分别是矩形四边的中点,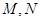 分别是
分别是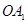 (其中
(其中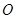 是坐标系原点)
是坐标系原点)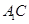 的中点,直线
的中点,直线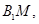
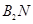 的交点为
的交点为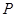 ,证明点
,证明点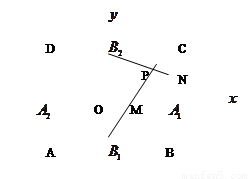
 ,
, 分别是直角三角形
分别是直角三角形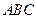 边
边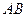 和
和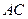 的中点,
的中点,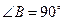 ,沿
,沿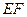 将三角形
将三角形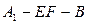 ,若
,若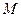 为线段
为线段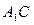 中点.求证:
中点.求证: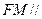 平面
平面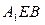 ;
;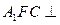 平面
平面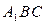 .
.

 ,
, 分别是直角三角形
分别是直角三角形 边
边 和
和 的中点,
的中点, ,沿
,沿 将三角形
将三角形 ,若
,若 为线段
为线段 中点.求证:
中点.求证: 平面
平面 ;
; 平面
平面 .
.