摘要:例1.一条直线过点(5.2).且在x轴.y轴上截距相等.则这直线方程为( ) A. B. C. D. 分析:设该直线在x轴.y轴上的截距均为a, 当a=0时.直线过原点.此时直线方程为, 当时.设直线方程为.方程为. 例2. 分析: 因此.只要根据已知条件.求出cosA.sinB即可得cosC的值.但是由sinA求cosA时.是一解还是两解?这一点需经过讨论才能确定.故解本题时要分类讨论.对角A进行分类. 解: 这与三角形的内角和为180°相矛盾. 例3.已知圆x2+y2=4.求经过点P(2.4).且与圆相切的直线方程. 分析:容易想到设出直线的点斜式方程y-4=k(x-2)再利用直线与圆相切的充要条件:“圆心到切线的距离等于圆的半径 .待定斜率k.从而得到所求直线方程.但要注意到:过点P的直线中.有斜率不存在的情形.这种情形的直线是否也满足题意呢?因此本题对过点P的直线分两种情形:斜率不存在- 解(略):所求直线方程为3x-4y+10=0或x=2 例4. 分析:解对数不等式时.需要利用对数函数的单调性.把不等式转化为不含对数符号的不等式.而对数函数的单调性因底数a的取值不同而不同.故需对a进行分类讨论. 解: 例5. 分析:解无理不等式.需要将两边平方后去根号.以化为有理不等式.而根据不等式的性质可知.只有在不等式两边同时为正时.才不改变不等号方向.因此应根据运算需求分类讨论.对x分类. 解: 例6. 分析:这是一个含参数a的不等式.一定是二次不等式吗?不一定.故首先对二次项系数a分类:.不等式易解,对于(1).又需再次分类:a>0或a<0.因为这两种情形下.不等式解集形式是不同的,不等式的解是在两根之外.还是在两根之间.而确定这一点之后.又会遇到1与谁大谁小的问题.因而又需作一次分类讨论.故而解题时.需要作三级分类. 解: 综上所述.得原不等式的解集为 ,, ,, . 例7.已知等比数列的前n项之和为.前n+1项之和为.公比q>0.令. 分析:对于等比数列的前n项和Sn的计算.需根据q是否为1分为两种情形: 故还需对q再次分类讨论. 解: 例8. 分析: 解:(1)当k=4时.方程变为4x2=0.即x=0.表示直线, (2)当k=8时.方程变为4y2=0.即y=0.表示直线, (i)当k<4时.方程表示双曲线,(ii)当4<k<6时.方程表示椭圆, (iii)当k=6时.方程表示圆,(iv)当6<k<8时.方程表示椭圆, (v)当k>8时.方程表示双曲线. 例9. 某车间有10名工人.其中4人仅会车工.3人仅会钳工.另外三人车工钳工都会.现需选出6人完成一件工作.需要车工.钳工各3人.问有多少种选派方案? 分析:如果先考虑钳工.因有6人会钳工.故有C63种选法.但此时不清楚选出的钳工中有几个是车钳工都会的.因此也不清楚余下的七人中有多少人会车工.因此在选车工时.就无法确定是从7人中选.还是从六人.五人或四人中选.同样.如果先考虑车工也会遇到同样的问题.因此需对全能工人进行分类: (1)选出的6人中不含全能工人,(2)选出的6人中含有一名全能工人,(3)选出的6人中含2名全能工人,(4)选出的6人中含有3名全能工人. 解:
网址:http://m.1010jiajiao.com/timu3_id_519884[举报]
求满足下列条件的直线方程,并化为一般式
(1)经过两点A(0,4)和B(4,0);
(2)经过点(-
,-
),与x轴平行;
(3)在x轴上的截距为4,斜率为直线y=
x-3的斜率的相反数;
(4)经过点(1,2),且与直线x-y+5=0垂直;
(5)过l1:3x-5y-10=0和l2:x+y+1=0的交点,且平行于l3:x+2y-5=0.
查看习题详情和答案>>
(1)经过两点A(0,4)和B(4,0);
(2)经过点(-
| 2 |
| 3 |
(3)在x轴上的截距为4,斜率为直线y=
| 1 |
| 2 |
(4)经过点(1,2),且与直线x-y+5=0垂直;
(5)过l1:3x-5y-10=0和l2:x+y+1=0的交点,且平行于l3:x+2y-5=0.
求满足下列条件的直线方程,并化为一般式
(1)经过两点A(0,4)和B(4,0);
(2)经过点(-
,-
),与x轴平行;
(3)在x轴上的截距为4,斜率为直线y=
x-3的斜率的相反数;
(4)经过点(1,2),且与直线x-y+5=0垂直;
(5)过l1:3x-5y-10=0和l2:x+y+1=0的交点,且平行于l3:x+2y-5=0.
查看习题详情和答案>>
(1)经过两点A(0,4)和B(4,0);
(2)经过点(-
| 2 |
| 3 |
(3)在x轴上的截距为4,斜率为直线y=
| 1 |
| 2 |
(4)经过点(1,2),且与直线x-y+5=0垂直;
(5)过l1:3x-5y-10=0和l2:x+y+1=0的交点,且平行于l3:x+2y-5=0.
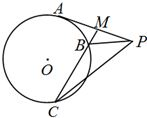 选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,
选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤.
A选修4-1:几何证明选讲
自圆O外一点P引圆的一条切线PA,切点为A,M为PA的中点,过点M引圆O的割线交该圆于B、C两点,且∠BMP=100°,∠BPC=40°,求∠MPB的大小.
B选修4-2:矩阵与变换
已知二阶矩阵A=
|
|
|
C选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线C的参数方程为
|
| π |
| 4 |
| 2 |
P为曲线C上的动点,求点P到直线l距离的最大值.
D选修4-5:不等式选讲
若正数a,b,c满足a+b+c=1,求
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |