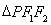摘要:[例1] 已知椭圆的左.右焦点分别是F1(-c.0).F2(c.0).Q是椭圆外的动点.满足点P是线段F1Q与该椭圆的交点.点T在线段F2Q上.并且满足 (Ⅰ)设为点P的横坐标.证明, (Ⅱ)求点T的轨迹C的方程, (Ⅲ)试问:在点T的轨迹C上.是否存在点M使△F1MF2的面积S=若存在.求∠F1MF2 的正切值,若不存在.请说明理由. 解 : (Ⅰ)证法一:设点P的坐标为 由P在椭圆上.得 由.所以 证法二:设点P的坐标为记 则 由 证法三:设点P的坐标为椭圆的左准线方程为 由椭圆第二定义得.即 由.所以 (Ⅱ)解法一:设点T的坐标为 当时.点(.0)和点(-.0)在轨迹上. 当|时.由.得. 又.所以T为线段F2Q的中点. 在△QF1F2中..所以有 综上所述.点T的轨迹C的方程是 解法二:设点T的坐标为 当时.点(.0)和点(-.0)在轨迹上. 当|时.由.得. 又.所以T为线段F2Q的中点. 设点Q的坐标为(). 则 因此 ① 由得 ② 将①代入②.可得 综上所述.点T的轨迹C的方程是 ③ ④ (Ⅲ)解法一:C上存在点M()使S=的充要条件是 由③得.由④得 所以.当时.存在点M.使S=, 当时.不存在满足条件的点M. 当时.. 由. . .得 解法二:C上存在点M()使S=的充要条件是 ③ ④ 由④得 上式代入③得 于是.当时.存在点M.使S=, 当时.不存在满足条件的点M. 当时.记. 由知.则 [例2] 已知椭圆C1的方程为.双曲线C2的左.右焦点分别为C1的左.右顶点.而C2的左.右顶点分别是C1的左.右焦点. (Ⅰ)求双曲线C2的方程, (Ⅱ)若直线与椭圆C1及双曲线C2都恒有两个不同的交点.且l与C2的两个交点A和B满足.求k的取值范围. 解:(Ⅰ)设双曲线C2的方程为.则 故C2的方程为 (Ⅱ)将代入得 由直线l与椭圆C1恒有两个不同的交点得 即 ① . 由直线l与双曲线C2恒有两个不同的交点A.B得 解此不等式得 ③ 由①.②.③得 故k的取值范围为 [例3](2005年·全国卷Ⅰ·理21文22) 已知椭圆的中心为坐标原点O.焦点在轴上.斜率为1且过椭圆右焦点F的直线交椭圆于A.B两点.与共线. (I)求椭圆的离心率, (II)设M为椭圆上任意一点.且.证明为定值. 解:(I)设椭圆方程为 则直线AB的方程为 化简得. 令 则 共线.得 知.所以椭圆可化为. 在椭圆上. 即 ① 由(I)知 又又.代入①得 故为定值.定值为1.
网址:http://m.1010jiajiao.com/timu3_id_519757[举报]
已知椭圆的左、右焦点分别为F1,F2,椭圆的离心率为
且经过点P(1,
).M为椭圆上的动点,以M为圆心,MF2为半径作圆M.
(1)求椭圆C的标准方程;
(2)若圆M与y轴有两个交点,求点M横坐标的取值范围;
(3)是否存在定圆N,使得圆N与圆M相切?若存在.求出圆N的方程;若不存在,说明理由.
查看习题详情和答案>>
| 1 |
| 2 |
| 3 |
| 2 |
(1)求椭圆C的标准方程;
(2)若圆M与y轴有两个交点,求点M横坐标的取值范围;
(3)是否存在定圆N,使得圆N与圆M相切?若存在.求出圆N的方程;若不存在,说明理由.
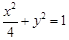 的左、右顶点分别为M、N,P为椭圆上任意一点,且直线PM的斜率的取值范围是[
的左、右顶点分别为M、N,P为椭圆上任意一点,且直线PM的斜率的取值范围是[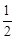 ,2],则直线PN的斜率的取值范围是( )
,2],则直线PN的斜率的取值范围是( )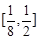 B.
B.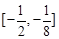 C.[-8,-2] D.[2,8]
C.[-8,-2] D.[2,8]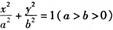 的左、右焦点分别为F1 F2,以F1 F2为直径的圆与椭圆在y轴左侧的部分交于A,B两点,且ΔF2AB是等边三角形,则椭圆的离心率为______
的左、右焦点分别为F1 F2,以F1 F2为直径的圆与椭圆在y轴左侧的部分交于A,B两点,且ΔF2AB是等边三角形,则椭圆的离心率为______ 在平面直角坐标系
在平面直角坐标系