摘要：4．直接法 例:如图.直线l1, l2相交于M.l1⊥l2.点N∈l1, 以A.B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若ΔAMN为锐角Δ.. |AN|=3.|BN|=6.建立适当坐标系.求曲线段C的方程. 分析:以l1为x轴.以MN的中垂线为y轴建立直角坐标系.如图. 由题意.曲线段C是以N为焦点.以l2为准线的抛物线的一部分. 其中A.B分别为C的端点. 由已知条件.可求方程为y2=8x
网址：http://m.1010jiajiao.com/timu3_id_519734[举报]
如图，直线l⊥平面α，垂足为O，已知△ABC中，∠ABC为直角，AB=2，BC=1，该直角三角形做符合以下条件的自由运动：（1）A∈l，（2）B∈α．则C、O两点间的最大距离为
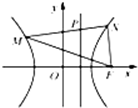（2012•资阳三模）如图，直线l与双曲线C：| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 1 |
| 2 |
（2007•崇明县一模）已知如图，直线l：x=-
（p＞0），点F(
，0)，P为平面上的动点，过P作直线l的垂线，垂足为点Q，且
•
=
•
．
（1）求动点P的轨迹C的方程；
（2）当p=2时，曲线C上存在不同的两点关于直线y=kx+3对称，求实数k满足的条件（写出关系式即可）；
（3）设动点M （a，0），过M且斜率为1的直线与轨迹C交于不同的两点A，B，线段AB的中垂线与x轴交于点N，当|AB|≤2p时，求△NAB面积的最大值．
查看习题详情和答案>>
| p |
| 2 |
| p |
| 2 |
| QP |
| QF |
| FP |
| FQ |
（1）求动点P的轨迹C的方程；
（2）当p=2时，曲线C上存在不同的两点关于直线y=kx+3对称，求实数k满足的条件（写出关系式即可）；
（3）设动点M （a，0），过M且斜率为1的直线与轨迹C交于不同的两点A，B，线段AB的中垂线与x轴交于点N，当|AB|≤2p时，求△NAB面积的最大值．
（2007•武汉模拟）如图，直线l：y=
如图，直线l⊥x轴，从原点开始向右平行移动到x=8处停止，它扫过△AOB 所得图形的面积为s，它与x轴的交点为（x，0）．