摘要:如图.在平面直角坐标系中.过轴正方向上一点任作一直线.与抛物线相交于两点.一条垂直于轴的直线.分别与线段和直线交于. (1)若.求的值, (2)若为线段的中点.求证:为此抛物线的切线, 的逆命题是否成立?说明理由. 解:(1)设过C点的直线为.所以.即.设A.=..因为.所以 .即. 所以.即所以 (2)设过Q的切线为..所以.即.它与的交点为M.又.所以Q.因为,所以.所以M,所以点M和点Q重合.也就是QA为此抛物线的切线. 的逆命题是成立.由(2)可知Q.因为PQ轴.所以 因为.所以P为AB的中点.
网址:http://m.1010jiajiao.com/timu3_id_519671[举报]
(本小题满分14分)如图,在一个由矩形 与正三角形
与正三角形 组合而成的平面图形中,
组合而成的平面图形中, 现将正三角形
现将正三角形 沿
沿 折成四棱锥
折成四棱锥 ,使
,使 在平面
在平面 内的射影恰好在边
内的射影恰好在边 上.
上.

(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
查看习题详情和答案>>
 (本小题满分14分)如图,在一个由矩形
(本小题满分14分)如图,在一个由矩形![]() 与正三角形
与正三角形![]() 组合而成的平面图形中,
组合而成的平面图形中,![]() 现将正三角形
现将正三角形![]() 沿
沿![]() 折成四棱锥
折成四棱锥![]() ,使
,使![]() 在平面
在平面![]() 内的射影恰好在边
内的射影恰好在边![]() 上.
上.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看习题详情和答案>>
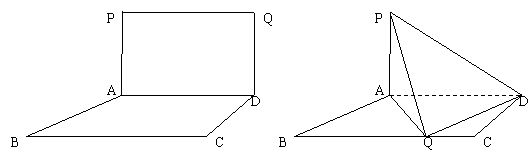 (本小题满分14分)如图,在直角梯形
(本小题满分14分)如图,在直角梯形 (本小题满分14分)如图,在直角梯形
(本小题满分14分)如图,在直角梯形 (本小题满分14分)如图,在一个由矩形
(本小题满分14分)如图,在一个由矩形