摘要:21. 设动点到点和的距离分别为和..且存在常数.使得. (1)证明:动点的轨迹为双曲线.并求出的方程, (2)过点作直线双曲线的右支于两点.试确定的范围.使.其中点为坐标原点. 解法一:(1)在中..即. .即. 点的轨迹是以为焦点.实轴长的双曲线. 方程为:. (2)设. ①当垂直于轴时.的方程为..在双曲线上. 即.因为.所以. ②当不垂直于轴时.设的方程为. 由得:. 由题意知:. 所以.. 于是:. 因为.且在双曲线右支上.所以 . 由①②知.. 解法二:(1)同解法一 (2)设..的中点为. ①当时.. 因为.所以, ②当时.. 又.所以, 由得.由第二定义得 . 所以. 于是由得 因为.所以.又. 解得:.由①②知. 江西文
网址:http://m.1010jiajiao.com/timu3_id_519664[举报]
(本小题满分12分) 设不等式组  表示的平面区域为
表示的平面区域为 ,区域
,区域 内的动点
内的动点 到直线
到直线 和直线
和直线 的距离之积为2, 记点
的距离之积为2, 记点 的轨迹为曲线
的轨迹为曲线 . 是否存在过点
. 是否存在过点 的直线l, 使之与曲线
的直线l, 使之与曲线 交于相异两点
交于相异两点 、
、 ,且以线段
,且以线段 为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
查看习题详情和答案>>
为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
查看习题详情和答案>>
 表示的平面区域为
表示的平面区域为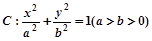 的离心率为
的离心率为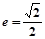 ,点
,点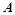 是椭圆上的一点,且点
是椭圆上的一点,且点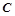 两焦点的距离之和为4.
两焦点的距离之和为4.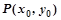 ,关于直线
,关于直线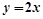 的对称点为
的对称点为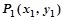 ,求
,求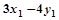 的取值范围.
的取值范围.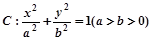 的离心率为
的离心率为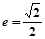 ,点
,点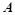 是椭圆上的一点,且点
是椭圆上的一点,且点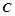 两焦点的距离之和为4.
两焦点的距离之和为4.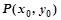 ,关于直线
,关于直线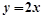 的对称点为
的对称点为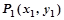 ,求
,求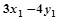 的取值范围.
的取值范围.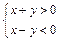 表示的平面区域为
表示的平面区域为 ,区域
,区域 到直线
到直线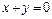 和直线
和直线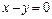 的距离之积为2, 记点
的距离之积为2, 记点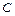 . 是否存在过点
. 是否存在过点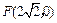 的直线l, 使之与曲线
的直线l, 使之与曲线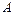 、
、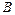 ,且以线段
,且以线段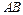 为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.