摘要:12.设分别是双曲线的左.右焦点.若点在双曲线上.且.则( ) A. B. C. D. 全国1理 (4)已知双曲线的离心率为.焦点是..则双曲线方程为( ) A. B. C. D. (11)抛物线的焦点为.准线为.经过且斜率为的直线与抛物线在轴上方的部分相交于点..垂足为.则的面积是( ) A. B. C. D. 已知椭圆的左.右焦点分别为..过的直线交椭圆于两点.过的直线交椭圆于两点.且.垂足为. (Ⅰ)设点的坐标为.证明:, (Ⅱ)求四边形的面积的最小值. (21)证明: (Ⅰ)椭圆的半焦距. 由知点在以线段为直径的圆上.故. 所以.. 当的斜率存在且时.的方程为.代入椭圆方程.并化简得. 设..则 . , 因为与相交于点.且的斜率为. 所以.. 四边形的面积 . 当时.上式取等号. (ⅱ)当的斜率或斜率不存在时.四边形的面积. 综上.四边形的面积的最小值为. 宁夏理
网址:http://m.1010jiajiao.com/timu3_id_519655[举报]
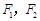 分别是双曲线
分别是双曲线 的左、右焦点.若点
的左、右焦点.若点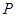 在双曲线上,且
在双曲线上,且 ,则
,则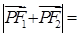
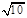 B.
B. C.
C. D.
D.
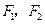 分别是双曲线
分别是双曲线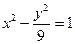 的左、右焦点.若点
的左、右焦点.若点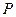 在双曲线上,且
在双曲线上,且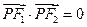 ,则
,则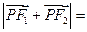 .
.