摘要:高考试题一般不要求特殊技巧.着重在“通性.通法 上.总结数学学科中解决问题的基本思想和方法.重点放在有价值的常规方法的应用上.特别是教材中每章节所给出的解决问题的一般方法.
网址:http://m.1010jiajiao.com/timu3_id_518929[举报]
设函数fn( θ )=sinnθ+( -1 )ncosnθ,0≤θ≤
,其中n为正整数.
(Ⅰ)判断函数f1(θ)、f3(θ)的单调性,并就f1(θ)的情形证明你的结论;
(Ⅱ)证明:2f6(θ)-f4(θ)=(cos4θ-sin4θ)(cos2θ-sin2θ);
(Ⅲ)试给出求函数fn(θ)的最大值和最小值及取得最值时θ的取值的一般规律(不要求给出证明).
查看习题详情和答案>>
| π |
| 4 |
(Ⅰ)判断函数f1(θ)、f3(θ)的单调性,并就f1(θ)的情形证明你的结论;
(Ⅱ)证明:2f6(θ)-f4(θ)=(cos4θ-sin4θ)(cos2θ-sin2θ);
(Ⅲ)试给出求函数fn(θ)的最大值和最小值及取得最值时θ的取值的一般规律(不要求给出证明).
| fn(θ) | fn(θ)的 单调性 |
fn(θ)的最小值及取得最小值时θ的取值 | fn(θ)的最大值及取得最大值时θ的取值 |
| n=1 | |||
| n=2 | |||
| n=3 | |||
| n=4 | |||
| n=5 | |||
| n=6 |
(2013·上海高考)如图,已知双曲线C1: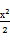 -y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
-y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.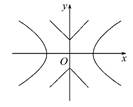
(1)在正确证明C1的左焦点是“C1-C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证).
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1-C2型点”.
(3)求证:圆x2+y2= 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.
设函数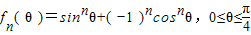 ,其中n为正整数.
,其中n为正整数.
(Ⅰ)判断函数f1(θ)、f3(θ)的单调性,并就f1(θ)的情形证明你的结论;
(Ⅱ)证明:2f6(θ)-f4(θ)=(cos4θ-sin4θ)(cos2θ-sin2θ);
(Ⅲ)试给出求函数fn(θ)的最大值和最小值及取得最值时θ的取值的一般规律(不要求给出证明).
查看习题详情和答案>>
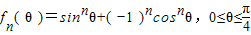 ,其中n为正整数.
,其中n为正整数.(Ⅰ)判断函数f1(θ)、f3(θ)的单调性,并就f1(θ)的情形证明你的结论;
(Ⅱ)证明:2f6(θ)-f4(θ)=(cos4θ-sin4θ)(cos2θ-sin2θ);
(Ⅲ)试给出求函数fn(θ)的最大值和最小值及取得最值时θ的取值的一般规律(不要求给出证明).
| fn(θ) | fn(θ)的 单调性 | fn(θ)的最小值及取得最小值时θ的取值 | fn(θ)的最大值及取得最大值时θ的取值 |
| n=1 | |||
| n=2 | |||
| n=3 | |||
| n=4 | |||
| n=5 | |||
| n=6 |
查看习题详情和答案>>
 是在
是在 上每一点均可导的函数,若
上每一点均可导的函数,若 在
在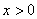 时恒成立.
时恒成立.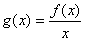 在
在 时,有
时,有 ;
;