摘要:39.过P(1.0)做曲线的切线.切点为Q1.设Q1在轴上的投影为P1.又过P1做曲线C的切线.切点为Q2.设Q2在轴上的投影为P2.-.依次下去得到一系列点Q1.Q2.Q3.-.Qn的横坐标为求证: (Ⅰ)数列是等比数列, (Ⅱ), (Ⅲ) 解:(Ⅰ)若切点是. 则切线方程为 当时.切线过点P(1.0)即得 当时.切线过点即得 ∴数列是首项为.公比为的等比数列. -6分 (Ⅱ) (Ⅲ)记. 则 两式相减
网址:http://m.1010jiajiao.com/timu3_id_518780[举报]
直线l:(m+1)x+2y-2m-2=0(m∈R)恒过定点C,以C为圆疏,2为半径作圆C,
(1)求圆C方程;
(2)设点C关于y轴的对称点为C1,动点M在曲线E上,在△MCC'中,满足∠C1MC=2θ,△MCC'的面积为4tanθ,求曲线E的方程;
(3)点P在(2)中的曲线E上,过点P做圆C的两条切线,切点为Q、R,求
的最小值.
查看习题详情和答案>>
(1)求圆C方程;
(2)设点C关于y轴的对称点为C1,动点M在曲线E上,在△MCC'中,满足∠C1MC=2θ,△MCC'的面积为4tanθ,求曲线E的方程;
(3)点P在(2)中的曲线E上,过点P做圆C的两条切线,切点为Q、R,求
| PQ• |
| PR |

 ,求点N到
,求点N到 对称的曲线方程
对称的曲线方程 到点M(-1,0)的距离与点P到点N(1,0)的距离之比为
到点M(-1,0)的距离与点P到点N(1,0)的距离之比为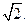
 ,求点N到
,求点N到 对称的曲线方程
对称的曲线方程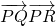 的最小值.
的最小值.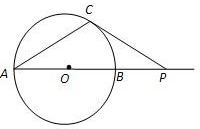 A.(不等式选讲选做题)若不等式|x+1|+|x-2|<a无实数解,则a的取值范围是
A.(不等式选讲选做题)若不等式|x+1|+|x-2|<a无实数解,则a的取值范围是