摘要: (本小题满分16分.第1小问满分5分.第2小问满分5分.第3小问满分6分) 已知在上有定义..且满足有.对数列有 (1) 证明:在上为奇函数. (2)求的表达式. (3)是否存在自然数.使得对于任意且<成立?若存在.求出的最小值.
网址:http://m.1010jiajiao.com/timu3_id_517820[举报]
(本小题满分16分,第1小题满分4分,第2小题满分5分,第3小
题满分7分)
(1)若对于任意的 ,总有
,总有 成立,求常数
成立,求常数 的值;
的值;
(2)在数列 中,
中, ,
, (
( ,
, ),求通项
),求通项 ;
;
(3)在(2)题的条件下,设 ,从数列
,从数列 中依次取出第
中依次取出第 项,第
项,第 项,…第
项,…第 项,按原来的顺序组成新的数列
项,按原来的顺序组成新的数列 ,其中
,其中 ,其中
,其中 ,
, .试问是否存在正整数
.试问是否存在正整数 使
使 且
且 成立?若存在,求正整数
成立?若存在,求正整数 的值;不存在,说明理由.
的值;不存在,说明理由.
查看习题详情和答案>>
(本小题满分16分,第1小题满分4分,第2小题满分5分,第3小
题满分7分)
(1)若对于任意的![]() ,总有
,总有![]() 成立,求常数
成立,求常数![]() 的值;
的值;
(2)在数列![]() 中,
中,![]() ,
,![]() (
(![]() ,
,![]() ),求证
),求证![]() 是等比数列,并求通项
是等比数列,并求通项![]() ;
;
(3)在(2)题的条件下,设![]() ,从数列
,从数列![]() 中依次取出第
中依次取出第![]() 项,第
项,第![]() 项,…第
项,…第![]() 项,按原来的顺序组成新的数列
项,按原来的顺序组成新的数列![]() ,其中
,其中![]() ,其中
,其中![]() .试问是否存在正整数
.试问是否存在正整数![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;不存在,说明理由.
的值;不存在,说明理由.
(本小题满分16分,第1小题满分4分,第2小题满分5分,第3小
题满分7分)
(1)若对于任意的![]() ,总有
,总有![]() 成立,求常数
成立,求常数![]() 的值;
的值;
(2)在数列![]() 中,
中,![]() ,
,![]() (
(![]() ,
,![]() ),求通项
),求通项![]() ;
;
(3)在(2)题的条件下,设![]() ,从数列
,从数列![]() 中依次取出第
中依次取出第![]() 项,第
项,第![]() 项,…第
项,…第![]() 项,按原来的顺序组成新的数列
项,按原来的顺序组成新的数列![]() ,其中
,其中![]() ,其中
,其中![]() ,
,![]() .试问是否存在正整数
.试问是否存在正整数![]() 使
使![]() 且
且![]() 成立?若存在,求正整数
成立?若存在,求正整数![]() 的值;不存在,说明理由.
的值;不存在,说明理由.
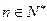 ,总有
,总有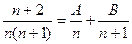 成立,求常数
成立,求常数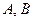 的值;
的值;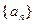 中,
中, ,
,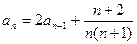 (
(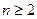 ,
,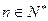 ),求通项
),求通项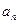 ;
;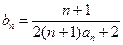 ,从数列
,从数列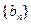 中依次取出第
中依次取出第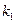 项,第
项,第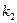 项,…第
项,…第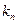 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列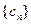 ,其中
,其中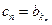 ,其中
,其中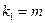 ,
,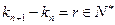 .试问是否存在正整数
.试问是否存在正整数 使
使 且
且 成立?若存
成立?若存 ,总有
,总有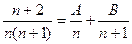 成立,求常数
成立,求常数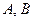 的值;
的值;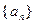 中,
中,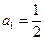 ,
, (
(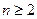 ,
,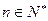 ),求通项
),求通项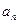 ;
;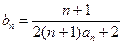 ,从数列
,从数列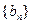 中依次取出第
中依次取出第 项,第
项,第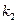 项,…第
项,…第 项,按原来的顺序组成新
项,按原来的顺序组成新 的数列
的数列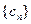 ,其中
,其中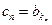 ,其中
,其中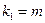 ,
,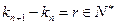 .试问是否存在正整数
.试问是否存在正整数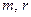 使
使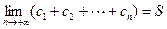 且
且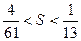 成立?若存
成立?若存