摘要：19．如图.已知三棱柱ABC-A1B1C1的棱长都是2.点A1与AB.AC的距离都等于.且A1E⊥B1B于E.A1F⊥C1C于F. (1)求证:平面A1EF⊥平面B1BCC1, (2)求点A到平面B1BCC1的距离, (3)求平面A1EF与平面A1B1C1所成二面角的大小. [解答](1).∴B1B平面A1EF.∴平面A1EF⊥平面B1BCC1, (2)由于A1A//平面B1BCC1. 故点A.A1与平面B1BCC1的距离相等. ∵四边形ABB1A1为菱形.故A1E=A1F=. ∵B1B⊥平面A1EF.EF平面A1EF. ∴BB1⊥EF.从而EF=BC=2. ∴△A1EF是等腰直角三角形. 取EF中点M.则A1M⊥EF.且A1M=1. 从而A1M⊥平面B1BCC1.即A1到平面B1BCC1的距离为1, (3)设平面A1EF与平面A1B1C1所成的二面角的棱为直线l.取B1C1的中点N. 则A1N⊥B1C1.但B1C1//EF.∴B1C1//平面A1EF.于是B1C1//l. 在△A1B1C1中.A1N=.∴A1M⊥l.A1N⊥l. 即∠MA1N为所求二面角的平面角. ∵A1M⊥平面B1BCC1.∴A1M⊥MN.∴cos∠NA1M=. 故所求二面角的大小为．
网址：http://m.1010jiajiao.com/timu3_id_517797[举报]
(本小题满分12分)
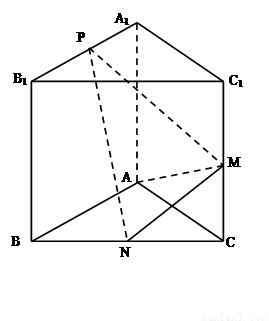
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1,且AB⊥AC，M是CC1的中点，N是BC的中点，点P在直线A1B1上，且满足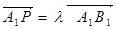
(1)证明：PN⊥AM
(2)若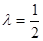
，求直线AA1与平面PMN所成角的正弦值.
查看习题详情和答案>>
(本小题满分12分)
如图，已知三棱柱ABC—A1B1C1的侧棱与底面垂直，AA1＝AB＝AC＝1，AB⊥AC，M、N分别是CC1、BC的中点，点P在A1B1上，且满足＝λ(λ∈R).
(1)证明：PN⊥AM；
(2)当λ取何值时，直线PN与平面ABC所成的角θ最大？并求该最大角的正切值；
(3)若平面PMN与平面ABC所成的二面角为45°，试确定点P的位置.
查看习题详情和答案>>
(本小题满分12分)
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1,且AB⊥AC，M是CC1的中点，N是BC的中点，点P在直线A1B1上，且满足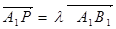
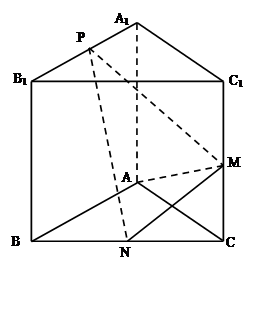
(1)证明：PN⊥AM
(2)若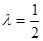
，求直线AA1与平面PMN所成角的正弦值.
＝λ
(λ∈R).
＝λ
(λ∈R).