摘要:在中.构成公差为正数的等差数列.且其周长为12,以为x轴. 的中垂线为 y轴.建立直角坐标系, (1)证明存在两定点E,F,使得|BE|+|BF|为定长,并求出点E,F的坐标及点B的轨迹C, (2)设P为轨迹C 上的任一点.点M,N分别在射线PA,PC上.动点Q满足.经过点A且以为方向向量的直 与动点Q的轨迹交于点R ,试问:是否存在一个定点 D.使得为定值?若存在求出点D的坐标,若不存在.说明理由?
网址:http://m.1010jiajiao.com/timu3_id_517644[举报]
等差数列{an}的首项和公差都是
,记{an}前n项和为Sn.等比数列{bn}各项均为正数,公比为q,记{bn}的前n项和为Tn.
(Ⅰ) 写出Si(i=1,2,3,4,5)构成的集合A;
(Ⅱ) 若q为正整数,问是否存在大于1的正整数k,使得Tk,T2k同时为集合A中的元素?若存在,写出所有符合条件的{bn}的通项公式;若不存在,请说明理由;
(Ⅲ) 若将Sn中的整数项按从小到大的顺序构成数列{cn},求{cn}的一个通项公式.
查看习题详情和答案>>
| 2 | 3 |
(Ⅰ) 写出Si(i=1,2,3,4,5)构成的集合A;
(Ⅱ) 若q为正整数,问是否存在大于1的正整数k,使得Tk,T2k同时为集合A中的元素?若存在,写出所有符合条件的{bn}的通项公式;若不存在,请说明理由;
(Ⅲ) 若将Sn中的整数项按从小到大的顺序构成数列{cn},求{cn}的一个通项公式.
设等差数列{an}的前n项和是Sn,已知S3=9,S6=36.
(1)求数列{an}的通项公式;
(2)是否存在正整数m、k,使am,am+5,ak成等比数列?若存在,求出m和k的值,若不存在,说明理由;
(3)设数列{bn}的通项公式为bn=3n-2.集合A={x|x=an,n∈N*},B={x|x=bn,n∈N*}.将集合A∪B中的元素从小到大依次排列,构成数列c1,c2,c3,…,求{cn}的通项公式.
查看习题详情和答案>>
(1)求数列{an}的通项公式;
(2)是否存在正整数m、k,使am,am+5,ak成等比数列?若存在,求出m和k的值,若不存在,说明理由;
(3)设数列{bn}的通项公式为bn=3n-2.集合A={x|x=an,n∈N*},B={x|x=bn,n∈N*}.将集合A∪B中的元素从小到大依次排列,构成数列c1,c2,c3,…,求{cn}的通项公式.
设等差数列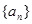 的公差
的公差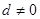 ,等比数列
,等比数列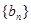 公比为
公比为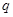 ,且
,且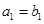 ,
,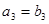 ,
,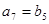
(1)求等比数列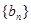 的公比
的公比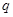 的值;
的值;
(2)将数列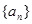 ,
,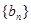 中的公共项按由小到大的顺序排列组成一个新的数列
中的公共项按由小到大的顺序排列组成一个新的数列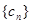 ,是否存在正整数
,是否存在正整数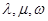 (其中
(其中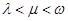 )使得
)使得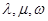 和
和 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组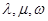 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看习题详情和答案>>
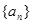 的公差
的公差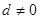 ,等比数列
,等比数列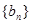 为公比为
为公比为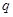 ,且
,且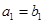 ,
,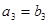 ,
,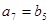 .
.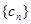 ,是否存在正整数
,是否存在正整数 (其中
(其中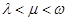 )使得
)使得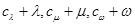 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组 的公差
的公差 ,等比数列
,等比数列 为公比为
为公比为 ,且
,且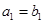 ,
, ,
, .
. ,是否存在正整数
,是否存在正整数 (其中
(其中 )使得
)使得 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组