摘要：21． 设=(a>0)为奇函数.且min=.数列{an}与{bn}满足 如下关系:a1=2. .． (1)求f(x)的解析表达式, (2) 证明:当n∈N+时. 有bn．
网址：http://m.1010jiajiao.com/timu3_id_517406[举报]
设
为奇函数, 且在(-∞, 0)内是减函数, f(-2)= 0, 则
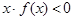的解集为 ( )
A． (-1, 0)∪(2, +∞) B．(-∞, -2)∪(0, 2 )
C． (-∞, -2)∪(2, +∞) D． (-2, 0)∪(0, 2 )
查看习题详情和答案>>
设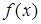
为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则
的解集为 ( )
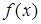为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则的解集为 ( ) | A．(-1, 0)∪(2, +∞) | B．(-∞, -2)∪(0, 2 ) |
| C．(-∞, -2)∪(2, +∞) | D．(-2, 0)∪(0, 2 ) |
为奇函数，对任意
均有
，已知
，则
等于
设为奇函数, 且在
内是减函数,
,则不等式
的解集为 ． 设
为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则
的解集为 ( )
| A．(-1, 0)∪(2, +∞) | B．(-∞, -2)∪(0, 2 ) |
| C．(-∞, -2)∪(2, +∞) | D．(-2, 0)∪(0, 2 ) |