摘要:21. 已知椭圆C1:=1的一条准线方程为.其左.右顶点分别是A.B,双曲线C2:=1的一条渐近线方程为3x-5y=0. (1)求椭圆C1的方程及双曲线C2的离心率. (2)在第一象限内.取双曲线C2上的一点P.连结AP交椭圆C1于点M.连结PB并延长交椭圆C1于点N.若AM=MP.求证:MN·AB=0
网址:http://m.1010jiajiao.com/timu3_id_517261[举报]
已知椭圆C1: =1(a>b>0)的左、右焦点分别为F1、F2,其中F2也是抛物线C2:y2=4x的焦点,M是C1与C2在第一象限的交点,且
=1(a>b>0)的左、右焦点分别为F1、F2,其中F2也是抛物线C2:y2=4x的焦点,M是C1与C2在第一象限的交点,且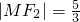
(I)求椭圆C1的方程; (II)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线7x-7y+1=0上,求直线AC的方程.
查看习题详情和答案>>
(2011•浙江)已知椭圆C1: =1(a>b>0)与双曲线C2:x2﹣
=1(a>b>0)与双曲线C2:x2﹣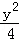 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
A.a2=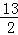 | B.a2=3 | C.b2= | D.b2=2 |
已知椭圆C1: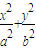 =1 (a>b>0)与双曲线C2:x2-
=1 (a>b>0)与双曲线C2:x2-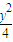 =1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
A.a2=
B.a2=3
C.b2=
D.b2=2
查看习题详情和答案>>
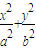 =1 (a>b>0)与双曲线C2:x2-
=1 (a>b>0)与双曲线C2:x2-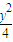 =1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )A.a2=

B.a2=3
C.b2=

D.b2=2
查看习题详情和答案>>
 =1和圆C:x2+y2=4,且圆C与x轴交于A1,A2两点.
=1和圆C:x2+y2=4,且圆C与x轴交于A1,A2两点. +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,直线l:x-y+
,直线l:x-y+ =0与椭圆C1相切.
=0与椭圆C1相切.