摘要：解:⑴由已知∴tan=2S,由<S<2,得1<tan<4.又∈(0,)∴⑵以O为原点,所在直线为X轴建立坐标系,设所求∵S△OFQ=︱︱•︱y0︱=c,∴︱y0︱=,∵=1,∴(c,0)•(x0-c,y0)=1,解得x0=c+.∴︱︱==,注意到当c≥2时,c+随c的增大而增大,因此当且仅当c=2时,︱︱有最小值,此时点Q坐标为(,-)或(,)∴解得,故所求椭圆方程为 专题4 平面向量(2)答案
网址：http://m.1010jiajiao.com/timu3_id_517120[举报]
（本小题满分12分）已知f (x)＝(1＋x)m＋(1＋2x)n(m，n∈N*)的展开式中x的系数为11.
(1)求x2的系数的最小值；
(2)当x2的系数取得最小值时，求f (x)展开式中x的奇次幂项的系数之和．
解： (1)由已知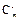
＋2
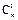＝11，∴m＋2n＝11，x2的系数为
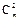＋22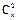
＝
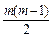＋2n(n－1)＝
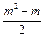＋(11－m)(
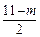－1)＝(m－
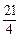)2＋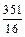
.
∵m∈N*，∴m＝5时，x2的系数取最小值22，此时n＝3.
(2)由(1)知，当x2的系数取得最小值时，m＝5，n＝3，
∴f (x)＝(1＋x)5＋(1＋2x)3.设这时f (x)的展开式为f (x)＝a0＋a1x＋a2x2＋…＋a5x5，
令x＝1，a0＋a1＋a2＋a3＋a4＋a5＝25＋
33，
令x＝－1，a0－a1＋a2－a3＋a4－a5＝－1，
两式相减得2(a1＋a3＋a5)＝60， 故展开式中x的奇次幂项的系数之和为30.
| |||||||||||
,1),N(1,
)(
,
是常数)，且
(O是坐标原点)．
关于
的函数关系式
；
,
］时，
的最小值为2，求
的值，并指出
的单调增区间和说明
(
)的图像可由
的图像经过怎样的变换而得到．
．