摘要:数列的通项的求法: ⑴公式法:①等差数列通项公式,②等比数列通项公式. ⑵已知(即)求.用作差法:. ⑶已知求.用作商法:. ⑷若求用累加法: . ⑸已知求.用累乘法: . ⑹已知递推关系求.用构造法. 特别地.(1)形如.(为常数)的递推数列都可以用待定系数法转化为公比为的等比数列后.再求. (2)形如的递推数列 都可以用倒数法求通项. 注意:(1)用求数列的通项公式时.你注意到此等式成立的条件了吗?(.当时.), (2)一般地当已知条件中含有与的混合关系时.常需运用关系式.先将已知条件转化为只含或的关系式.然后再求解.
网址:http://m.1010jiajiao.com/timu3_id_516874[举报]
设数列{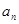 }的前n项和
}的前n项和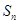 满足:
满足: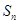 =n
=n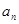 -2n(n-1).等比数列{
-2n(n-1).等比数列{ }的前n项和为
}的前n项和为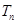 ,公比为
,公比为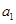 ,且
,且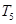 =
=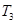 +2
+2 .
.
(1)求数列{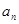 }的通项公式;
}的通项公式;
(2)设数列{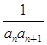 }的前n项和为
}的前n项和为 ,求证:
,求证: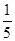 ≤
≤ <
<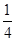 .
.
【解析】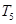 =
=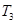 +2
+2 求出
求出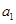 ,由
,由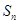 =n
=n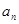 -2n(n-1)递写一个式子相减,得{
-2n(n-1)递写一个式子相减,得{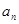 }为等差数列;(2)裂项法求
}为等差数列;(2)裂项法求 ,然后证明
,然后证明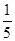 ≤
≤ <
<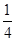 .
.
查看习题详情和答案>>
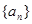 的前n项和为
的前n项和为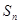 ,且
,且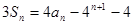
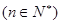 ,令
,令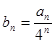 .
.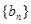 是等差数列,并求数列
是等差数列,并求数列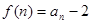
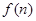 是18的倍数.
是18的倍数. 的前n项和为
的前n项和为 ,且
,且
 ,令
,令 .
. 是等差数列,并求数列
是等差数列,并求数列
 是18的倍数.
是18的倍数.