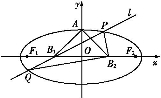
摘要:如图1.设P.Q为△ABC内的两点.且. =+则△ABP的面积与△ABQ的面积之比为 ( B ) A. B. C. D. 图1 图2 解:如图2设,则由平行四边形法则知NP∥AB.所以=.同理可得. 故即选B.
网址:http://m.1010jiajiao.com/timu3_id_516859[举报]
 一块边长为10的正方形纸片,按如图所示将阴影部分裁下,然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD(底面是正方形,顶点在底面的射影是底面中心的四棱锥).
一块边长为10的正方形纸片,按如图所示将阴影部分裁下,然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD(底面是正方形,顶点在底面的射影是底面中心的四棱锥).(1)过此棱锥的高以及一底边中点F作棱锥的截面(如图),设截面三角形面积为y,求y的最大值及y取最大值时的x的值;
(2)空间一动点P满足
| SP |
| SA |
| SB |
| SC |
| SP |
(3)在第(1)问的条件下,设F是CD的中点,问是否存在这样的动点Q,它在此棱锥的表面(包含底面ABCD)运动,且FQ⊥AC?如果存在,计算其运动轨迹的长度,如果不存在,说明理由.
 如图,椭圆
如图,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 1 |
| 4 |
(1)求椭圆的方程;
(2)试证:对于所有满足条件的P,Q,恒有|RP|=|RQ|;
(3)试判断△PQR能否为等边三角形?证明你的结论.
 (2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
(2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
| ||
| 2 |
| ||
| 2 |
(1)求椭圆C的方程;
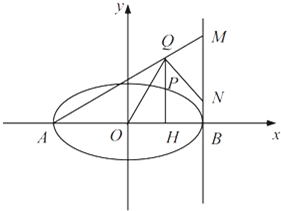
(2)如图,椭圆C 的长轴为AB,设 P 是椭圆上异于 A、B 的任意一点,PH⊥x轴,H为垂足,点Q 满足
| PQ |
| HP |
| BM |
| BN |
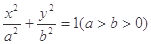 的长轴为AB,过点B的直线
的长轴为AB,过点B的直线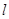 与
与
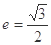 ,F为椭圆的左焦点,且
,F为椭圆的左焦点,且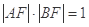
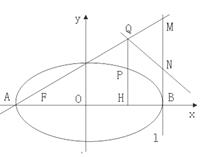
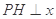 轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线
轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线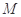 ,
,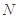 为
为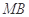 的中点,判定直线
的中点,判定直线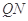 与以
与以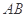 为直径的圆O位置关系。
为直径的圆O位置关系。