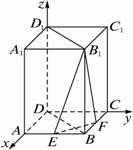
摘要：12．正四棱柱ABCD-A1B1C1D1中.底面边长为.侧棱长为.E.F分别是AB1.CB1的中点.求证:平面D1EF⊥平面AB1C. 联想:直四棱柱ABCD-A1B1C1D1的底面是菱形.AD=AA1=a.∠DAB=600.E.F为AA1.CC1的中点. (Ⅰ)证明:面B1EF⊥平面BDD1,(Ⅱ)求直四棱 柱被面DEB1F所截得的下半部分的体积, (Ⅲ)求面DEB1F与底面A1B1C1D1所成的二面角.
网址：http://m.1010jiajiao.com/timu3_id_516835[举报]
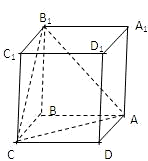正四棱柱ABCD-A1B1C1D1中，底面边长为
，侧棱长为4．
（1）求证：平面AB1C⊥平面BDD1B1；
（2）求D1到面AB1C的距离；
（3）求三棱锥D1-ACB1的体积V．
查看习题详情和答案>>
正四棱柱ABCD-A1B1C1D1中，底面边长为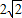
，侧棱长为4．
（1）求证：平面AB1C⊥平面BDD1B1；
（2）求D1到面AB1C的距离；
（3）求三棱锥D1-ACB1的体积V．
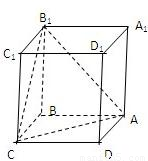查看习题详情和答案>>
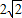，侧棱长为4．（1）求证：平面AB1C⊥平面BDD1B1；
（2）求D1到面AB1C的距离；
（3）求三棱锥D1-ACB1的体积V．
查看习题详情和答案>>
正四棱柱ABCD-A1B1C1D1中，底面边长为2| 2 |
（1）求证：平面AB1C⊥平面BDD1B1；
（2）求D1到面AB1C的距离；
（3）求三棱锥D1-ACB1的体积V． 查看习题详情和答案>>
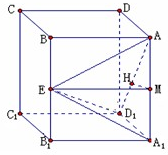正四棱柱ABCD-A1B1C1D1中，底面边长为a，侧棱AA1长为ka（k＞0），E为侧棱BB1的中点，记以AD1为棱，EAD1，A1AD1为面的二面角大小为θ．
，侧棱长为4，E、F分别为棱AB、BC的中点.