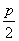摘要:已知抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A.B.且|AB|≤2p. (1)求a的取值范围. (2)若线段AB的垂直平分线交x轴于点N.求△NAB面积的最大值. 解:(1)设直线l的方程为:y=x-a,代入抛物线方程得(x-a)2=2px,即x2-2(a+p)x+a2=0 ∴|AB|=≤2p.∴4ap+2p2≤p2,即4ap≤-p2 又∵p>0,∴a≤-. (2)设A(x1,y1).B(x2,y2).AB的中点 C(x,y), 由(1)知.y1=x1-a,y2=x2-a,x1+x2=2a+2p, 则有x==p. ∴线段AB的垂直平分线的方程为y-p=-(x-a-p),从而N点坐标为(a+2p,0)? 点N到AB的距离为 从而S△NAB= 当a有最大值-时.S有最大值为p2.
网址:http://m.1010jiajiao.com/timu3_id_516470[举报]
已知抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,且|AB|≤2p.
(1)求a的取值范围.
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
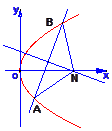
已知抛物线y2=2px(p>0)过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,|AB|≤2p.
(1)求实数a的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
查看习题详情和答案>>
已知抛物线y2=2px(p>0),若有过动点M(a,0)且斜率为1的直线l与抛物线交于不同两点A、B,|AB|≤2p.(1)求a的取值范围;(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
查看习题详情和答案>>