摘要:8.已知函数在点处取得极大值.其导函数的图象经过点..如图所示.求:(Ⅰ)的值, (Ⅱ)的值. 解析:解法一: (Ⅰ)由图象可知.在上,在(1,2)上,在上, 故在,上递增,在(1,2)上递减,因此在处取得极大值,所以. (Ⅱ)由 得解得 解法二:(Ⅰ)同解法一. (Ⅱ)设又 所以 由,即得, 所以. 9.已知函数. (I)讨论函数的单调性, (Ⅱ)若曲线上两点A.B处的切线都与y轴垂直.且线段AB与x轴有公共点.求实数a的取值范围. 解 (Ⅰ)由题设知.令. 当(i)a>0时. 若.则.所以在区间上是增函数, 若.则.所以在区间上是减函数, 若.则.所以在区间上是增函数, (i i)当a<0时. 若.则.所以在区间上是减函数, 若.则.所以在区间上是减函数, 若.则.所以在区间上是增函数, 若.则.所以在区间上是减函数. 的讨论及题设知.曲线上的两点A.B的纵坐标为函数的极值.且函数在处分别是取得极值.. 因为线段AB与x轴有公共点.所以.即 .所以. 故. 解得 -1≤a<0或3≤a≤4.即所求实数a的取值范围是[-1.0)∪[3.4].
网址:http://m.1010jiajiao.com/timu3_id_516010[举报]

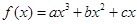 在点
在点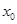 处取得极大值
处取得极大值 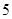 ,其导函数
,其导函数 的图象经过点
的图象经过点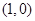 ,
,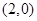 ,如图所示.求:
,如图所示.求:
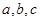 的值.
的值.