摘要： 解:∵侧面A1ACC1⊥底面ABC.作A1O⊥AC于点O. ∴A1O⊥平面ABC. 又∠ABC=∠A1AC=60°.且各棱长都相等. ∴AO=1.OA1=OB= .BO⊥AC. 故以O为坐标原点.建立如图所示的空间直角坐标系O-xyz,则 A.A1.C. ∴ . 设平面AB1C的法向量为n=(x,y,1) 则 解得n=. 由cos< >= 而侧棱AA1与平面AB1C所成角.即是向量 与平面AB1C的法向量所成锐角的余角. ∴侧棱AA1与平面AB1C所成角的大小为arcsin (Ⅱ) ∵ 而 ∴ 又∵B.∴点D的坐标为D. 假设存在点P符合题意.则点P的坐标可设为P. ∴ ∵DP∥平面AB1C.n=为平面AB1C的法向量. ∴由 .得 又DP 平面AB1C. 故存在点P.使DP∥平面AB1C.其从标为.即恰好为A1点.
网址：http://m.1010jiajiao.com/timu3_id_515557[举报]
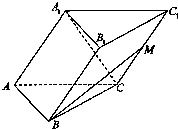已知斜三棱柱ABC-A1B1C1的底面为正三角形，侧面A1ACC1为菱形，∠A1AC=60°，且平面A1ACC1⊥平面ABC，M是C1C的中点．（1）求证：A1C⊥BM；
（2）求二面角B-A1A-C的正切值．
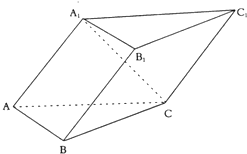已知斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直，∠ABC=90°，BC=2，AC=2| 3 |
①求侧面A1ABB1与底面ABC所成锐二面角的大小；
②求顶点C到侧面A1ABB1的距离．
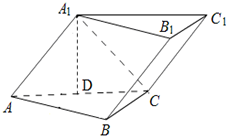如图，已知斜三棱柱（侧棱不垂直于底面）ABC-A1B1C1的侧面A1ACC1与底面ABC垂直，BC=2，AC=2| 3 |
| 2 |
| 6 |
（Ⅰ） 设AC的中点为D，证明A1D⊥底面ABC；
（Ⅱ） 求异面直线A1C与AB成角的余弦值．
（2012•肇庆一模）如图，已知斜三棱柱（侧棱不垂直于底面）ABC-A1B1C1的侧面A1ACC1与底面ABC垂直，BC=2，AC=2