摘要：19． (1)由 ①当0<k<1时.得, ②当k=1时.得 ③当k>1时.得 综上所求函数的定义域:当0<k<1时为时为 (2)由上是增函数 得k> 又对任意的..当时. 有得: 易求得k的取值范围是()
网址：http://m.1010jiajiao.com/timu3_id_515399[举报]
时,方程
=kx的解的个数是( )
（2009•普陀区一模）如图，已知圆C：x2+y2=r2与x轴负半轴的交点为A．由点A出发的射线l的斜率为k，且k为有理数．射线l与圆C相交于另一点B．（1）当r=1时，试用k表示点B的坐标；
（2）当r=1时，试证明：点B一定是单位圆C上的有理点；（说明：坐标平面上，横、纵坐标都为有理数的点为有理点．我们知道，一个有理数可以表示为
| q | p |
（3）定义：实半轴长a、虚半轴长b和半焦距c都是正整数的双曲线为“整勾股双曲线”．
当0＜k＜1时，是否能构造“整勾股双曲线”，它的实半轴长、虚半轴长和半焦距的长恰可由点B的横坐标、纵坐标和半径r的数值构成？若能，请尝试探索其构造方法；若不能，试简述你的理由．
某种商品，现在定价p元，每月卖出n件，设定价上涨x成，每月卖出数量减少y成，每月售货总金额变成现在的z倍．
(1)用x和y表示z；
(2)设x与y满足y＝kx(0<k<1)，利用k表示当每月售货总金额最大时x的值；
(3)若y＝
x，求使每月售货总金额有所增加的x值的范围．
成立，且f（a） = 1（a为正常数），当0 < x < 2a时，f（x） > 0．（I）判断f（x）奇偶性；（II）证明f（x）为周期函数；（III）求f （x）在[2a，3a] 上的最小值和最大值．
时，数列{an}为递减数列；
时，数列{an}不一定有最大项；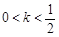
时，数列{an}为递减数列；
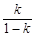为正整数时，数列{an}必有两项相等的最大项.