摘要：14．函数的图象的一条对称轴的方程是() 正确答案A 错因:没能观察表达式的整体构造.盲目化简导致表达式变繁而无法继续化简.
网址：http://m.1010jiajiao.com/timu3_id_515107[举报]
已知函数f（x）=1+sinxcosx，g(x)=cos2(x+
)．
（I）设x=x0是函数y=f（x）的图象上一条对称轴，求g(
)的值；
（II）求使函数h(x)=f(
)+g(
)(ω＞0)在区间[-
，
]上是增函数的ω的最大值．
查看习题详情和答案>>
| π |
| 12 |
（I）设x=x0是函数y=f（x）的图象上一条对称轴，求g(
| x | 0 |
（II）求使函数h(x)=f(
| ωx |
| 2 |
| ωx |
| 2 |
| 2π |
| 3 |
| π |
| 3 |
已知函数f(x)=1+sinxcosx，g(x)=cos2(x+
)
（1）设x=x0是函数y=f（x）的图象上一条对称轴，求g(
)的值．
（2）求使函数h(x)=f(
)+g(
)，(ω＞0)，在区间[-
，
]上是增函数的ω的最大值．
查看习题详情和答案>>
| π |
| 12 |
（1）设x=x0是函数y=f（x）的图象上一条对称轴，求g(
| x | 0 |
（2）求使函数h(x)=f(
| ωx |
| 2 |
| ωx |
| 2 |
| 2π |
| 3 |
| π |
| 3 |
+
)(k≠0)的图象有一条对称轴为x=
,求k;
)的对称轴与对称中心.
．
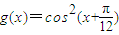的值；
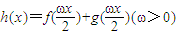在区间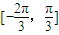
上是增函数的ω的最大值．