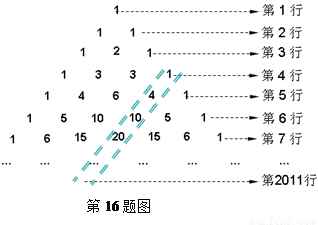
摘要：如下图.观察前两行图形.第三行“? 处应填 ? A. B. C D
网址：http://m.1010jiajiao.com/timu3_id_514838[举报]
如下图所示，是树形图形.第一层是一条与水平线垂直的线段，长度为1；第二层在第一层线段的前端作两条与该段均成135°的线段，长度为其一半；第三层按第二层的方法在每一线段的前端生成两条线段；重复前面的做法作图至第n层.设树形图的第n层的最高点到水平线的距离为第n层树形图的高度.
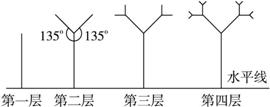
（1）求第三层及第四层树形图的高度H3，H4；
（2）求第n层树形图的高度Hn;
（3）若树形图的高度大于2，则称树形图为“高大”，否则称为“矮小”.显然，当n=1,2时是“矮小”的，是否存在m∈Z使得当n＞m时，该树形图是“高大”的？
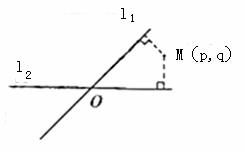
查看习题详情和答案>>
如下图所示，两射线OA与OB交于点O，下列5个向量中，①2
| OA |
| OB |
| 3 |
| 4 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 2 |
| OA |
| 1 |
| 3 |
| OB |
| 3 |
| 4 |
| OA |
| 1 |
| 5 |
| OB |
| 3 |
| 4 |
| OA |
| 1 |
| 5 |
| OB |
若以O为起点，终点落在阴影区域内（含边界）的向量有（ ）个．
查看习题详情和答案>>
某同学由于求不出积分
lnxdx的准确值，于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分
lnxdx．他用计算机分别产生10个在[1，e]上的均匀随机数xi（1≤i≤10）和10个在[0，1]上的均匀随机数yi（1≤i≤10），其数据记录为如下表的前两行
则依此表格中的数据，可得积分
lnxdx的一个近似值为
(e-1)
(e-1)．
查看习题详情和答案>>
| ∫ | e 1 |
| ∫ | e 1 |
| x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| lnx | 0.92 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
| ∫ | e 1 |
| 3 |
| 5 |
| 3 |
| 5 |
）．
