题目内容
某同学由于求不出积分
lnxdx的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分
lnxdx.他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行
则依此表格中的数据,可得积分
lnxdx的一个近似值为
(e-1)
(e-1).
| ∫ | e 1 |
| ∫ | e 1 |
| x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| lnx | 0.92 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
| ∫ | e 1 |
| 3 |
| 5 |
| 3 |
| 5 |
分析:由题意,得到10个点(xi,yi)(i=1,2,…,N),其中满足yi≤f(xi)(i=1,2,…,N)的点有6个,利用几何概型求概率,即可得到结论.
解答:解:由题意,得到10个点(xi,yi)(i=1,2,…,N),其中满足yi≤f(xi)(i=1,2,…,N)的点有6个,
∴
=
=
∴
lnxdx=
(e-1)
故答案为:
(e-1)
∴
| ||
| e-1 |
| 6 |
| 10 |
| 3 |
| 5 |
∴
| ∫ | e 1 |
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题考查几何概型模拟估计定积分值,以及定积分在面积中的简单应用,属于基础题.

练习册系列答案
相关题目
某同学由于求不出积分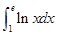 的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分
的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分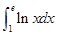 .他用计算机分别产生
.他用计算机分别产生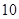 个在
个在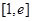 上的均匀随机数
上的均匀随机数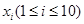 和
和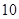 个在
个在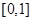 上的均匀随机数
上的均匀随机数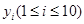 ,其数据记录为如下表的前两行.
,其数据记录为如下表的前两行.
|
x |
2.50 |
1.01 |
1.90 |
1.22 |
2.52 |
2.17 |
1.89 |
1.96 |
1.36 |
2.22 |
|
y |
0.84 |
0.25 |
0.98 |
0.15 |
0.01 |
0.60 |
0.59 |
0.88 |
0.84 |
0.10 |
|
lnx |
0.92 |
0.01 |
0.64 |
0.20 |
0.92 |
0.77 |
0.64 |
0.67 |
0.31 |
0.80 |
则依此表格中的数据,可得积分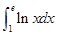 的一个近似值为
.
的一个近似值为
.
某同学由于求不出积分 的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分
的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分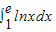 .他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行
.他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行
则依此表格中的数据,可得积分 的一个近似值为 .
的一个近似值为 .
 的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分
的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分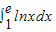 .他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行
.他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行 | x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| lnx | 0.92 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
 的一个近似值为 .
的一个近似值为 .
某同学由于求不出积分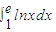 的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分
的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分 .他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行
.他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行
则依此表格中的数据,可得积分 的一个近似值为 .
的一个近似值为 .
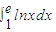 的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分
的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分 .他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行
.他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行 | x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| lnx | 0.92 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
 的一个近似值为 .
的一个近似值为 .
某同学由于求不出积分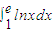 的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分
的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分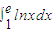 .他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行
.他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行
则依此表格中的数据,可得积分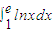 的一个近似值为 .
的一个近似值为 .
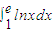 的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分
的准确值,于是他采用“随机模拟方法”和利用“积分的几何意义”来近似计算积分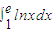 .他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行
.他用计算机分别产生10个在[1,e]上的均匀随机数xi(1≤i≤10)和10个在[0,1]上的均匀随机数yi(1≤i≤10),其数据记录为如下表的前两行 | x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| lnx | 0.92 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
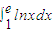 的一个近似值为 .
的一个近似值为 .