摘要：21．已知曲线C:xy=1.过C上一点作一斜率为的直线交曲线C于另一点.点列的横坐标构成数列{}.其中. (I)求与的关系式, (II)求证:{}是等比数列, (Ⅲ)求证:.
网址：http://m.1010jiajiao.com/timu3_id_514637[举报]
已知曲线C：xy=1，过C上一点A1（x1，y1）作斜率k1的直线，交曲线C于另一点A2（x2，y2），再过A2（x2，y2）作斜率为k2的直线，交曲线C于另一点A3（x3，y3），…，过An（xn，yn）作斜率为kn的直线，交曲线C于另一点An+1（xn+1，yn+1）…，其中x1=1，kn=-
(x∈N*)
（1）求xn+1与xn的关系式；
（2）判断xn与2的大小关系，并证明你的结论；
（3）求证：|x1-2|+|x2-2|+…+|xn-2|＜2． 查看习题详情和答案>>
| xn+1 | ||
|
（1）求xn+1与xn的关系式；
（2）判断xn与2的大小关系，并证明你的结论；
（3）求证：|x1-2|+|x2-2|+…+|xn-2|＜2． 查看习题详情和答案>>
已知曲线C：xy=1，过C上一点An（xn，yn）作一斜率kn=-
的直线交曲线C于另一点An+1（xn+1，yn+1）．
（1）求xn与xn+1之间的关系式；
（2）若x1=
，求证：数列
+
是等比数列；
（3）求证：（-1）x1+（-1）2x2+（-1）3x3+…（-1）nxn＜1（n∈N*）
查看习题详情和答案>>
| 1 |
| xn+2 |
（1）求xn与xn+1之间的关系式；
（2）若x1=
| 11 |
| 7 |
| 1 |
| xn-2 |
| 1 |
| 3 |
（3）求证：（-1）x1+（-1）2x2+（-1）3x3+…（-1）nxn＜1（n∈N*）
已知曲线C：xy=1，过C上一点An（xn，yn）作一斜率为kn=-
的直线交曲线C于另一点An+1（xn+1，yn+1），点列An（n=1，2，3，…）的横坐标构成数列{xn}，其中x1=
．
（1）求xn与xn+1的关系式；
（2）求证：{
+
}是等比数列；
（3）求证：（-1）x1+（-1）2x2+（-1）3x3+…+（-1）nxn＜1（n∈N，n≥1）． 查看习题详情和答案>>
| 1 |
| xn+2 |
| 11 |
| 7 |
（1）求xn与xn+1的关系式；
（2）求证：{
| 1 |
| xn-2 |
| 1 |
| 3 |
（3）求证：（-1）x1+（-1）2x2+（-1）3x3+…+（-1）nxn＜1（n∈N，n≥1）． 查看习题详情和答案>>
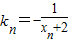的直线交曲线C于另一点An+1（xn+1，yn+1），点列An（n=1，2，3，…）的横坐标构成数列{xn}，其中
．
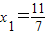}是等比数列；