摘要:20.(Ⅰ)解:.是直线与双曲线两条渐近线的交点. . 即------2分 双曲线的焦距为4.--------4分 解得. 椭圆方程为----5分 (Ⅱ)解:设椭圆的焦距为.则点的坐标为 . 直线的斜率为.直线的斜率为. 直线的方程为----------------7分 由 解得 即点 设由. 得 即 --10分. 点在椭圆上.------------12分 即 . 椭圆的离心率是 --------14分
网址:http://m.1010jiajiao.com/timu3_id_513944[举报]
已知双曲线C的中心在原点,D(1,0)是它的一个顶点,
=(1,
)是它的一条渐近线的一个方向向量.
(1)求双曲线C的方程;
(2)若过点(-3,0)任意作一条直线与双曲线C交于A,B两点 (A,B都不同于点D),求证:
•
为定值;
(3)对于双曲线Γ:
-
=1(a>0,b>0,a≠b),E为它的右顶点,M,N为双曲线Γ上的两点(都不同于点E),且EM⊥EN,那么直线MN是否过定点?若是,请求出此定点的坐标;若不是,说明理由.然后在以下三个情形中选择一个,写出类似结论(不要求书写求解或证明过程).
情形一:双曲线
-
=1(a>0,b>0,a≠b)及它的左顶点;
情形二:抛物线y2=2px(p>0)及它的顶点;
情形三:椭圆
+
=1(a>b>0)及它的顶点.
查看习题详情和答案>>
| d |
| 2 |
(1)求双曲线C的方程;
(2)若过点(-3,0)任意作一条直线与双曲线C交于A,B两点 (A,B都不同于点D),求证:
| DA |
| DB |
(3)对于双曲线Γ:
| x2 |
| a2 |
| y2 |
| b2 |
情形一:双曲线
| x2 |
| a2 |
| y2 |
| b2 |
情形二:抛物线y2=2px(p>0)及它的顶点;
情形三:椭圆
| x2 |
| a2 |
| y2 |
| b2 |
(2013•松江区二模)已知双曲线C的中心在原点,D(1,0)是它的一个顶点,
=(1,
)是它的一条渐近线的一个方向向量.
(1)求双曲线C的方程;
(2)若过点(-3,0)任意作一条直线与双曲线C交于A,B两点 (A,B都不同于点D),求证:
•
为定值;
(3)对于双曲线Γ:
-
=1(a>0,b>0,a≠b),E为它的右顶点,M,N为双曲线Γ上的两点(都不同于点E),且EM⊥EN,那么直线MN是否过定点?若是,请求出此定点的坐标;若不是,说明理由.然后在以下三个情形中选择一个,写出类似结论(不要求书写求解或证明过程).
情形一:双曲线
-
=1(a>0,b>0,a≠b)及它的左顶点;
情形二:抛物线y2=2px(p>0)及它的顶点;
情形三:椭圆
+
=1(a>b>0)及它的顶点.
查看习题详情和答案>>
| d |
| 2 |
(1)求双曲线C的方程;
(2)若过点(-3,0)任意作一条直线与双曲线C交于A,B两点 (A,B都不同于点D),求证:
| DA |
| DB |
(3)对于双曲线Γ:
| x2 |
| a2 |
| y2 |
| b2 |
情形一:双曲线
| x2 |
| a2 |
| y2 |
| b2 |
情形二:抛物线y2=2px(p>0)及它的顶点;
情形三:椭圆
| x2 |
| a2 |
| y2 |
| b2 |
 =
=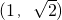 是它的一条渐近线的一个方向向量.
是它的一条渐近线的一个方向向量.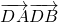 为定值;
为定值;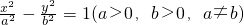 ,E为它的右顶点,M,N为双曲线Γ上的两点(都不同于点E),且EM⊥EN,那么直线MN是否过定点?若是,请求出此定点的坐标;若不是,说明理由.然后在以下三个情形中选择一个,写出类似结论(不要求书写求解或证明过程).
,E为它的右顶点,M,N为双曲线Γ上的两点(都不同于点E),且EM⊥EN,那么直线MN是否过定点?若是,请求出此定点的坐标;若不是,说明理由.然后在以下三个情形中选择一个,写出类似结论(不要求书写求解或证明过程). 及它的顶点.
及它的顶点.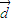 =
=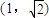 是它的一条渐近线的一个方向向量.
是它的一条渐近线的一个方向向量.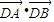 为定值;
为定值;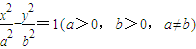 ,E为它的右顶点,M,N为双曲线Γ上的两点(都不同于点E),且EM⊥EN,那么直线MN是否过定点?若是,请求出此定点的坐标;若不是,说明理由.然后在以下三个情形中选择一个,写出类似结论(不要求书写求解或证明过程).
,E为它的右顶点,M,N为双曲线Γ上的两点(都不同于点E),且EM⊥EN,那么直线MN是否过定点?若是,请求出此定点的坐标;若不是,说明理由.然后在以下三个情形中选择一个,写出类似结论(不要求书写求解或证明过程).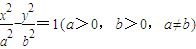 及它的左顶点;
及它的左顶点;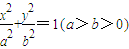 及它的顶点.
及它的顶点.