摘要:(理) 如果学生甲每次投篮投中的概率为.那么他连续投三次.恰好两次投中的概率为 .至少有一次投中的概率为 . 的图像与f(x)=ax-1的图像关于直线y=x对称.若g.则g(a-1)的值为 .
网址:http://m.1010jiajiao.com/timu3_id_513654[举报]
在某校组织的一次篮球定点投篮测试中,规定每人最多投 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得 分,在
分,在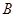 处每投进一球得
处每投进一球得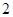 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用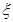 表示,如果
表示,如果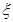 的值不低于
的值不低于 分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在
分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在 处投一球,以后都在
处投一球,以后都在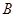 处投;方案2:都在
处投;方案2:都在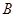 处投篮.甲同学在
处投篮.甲同学在 处投篮的命中率为
处投篮的命中率为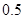 ,在
,在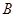 处投篮的命中率为
处投篮的命中率为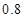 .
.
(Ⅰ)甲同学选择方案1.
求甲同学测试结束后所得总分等于4的概率;
求甲同学测试结束后所得总分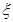 的分布列和数学期望
的分布列和数学期望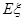 ;
;
(Ⅱ)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看习题详情和答案>>
在某校组织的一次篮球定点投篮测试中,规定每人最多投 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得 分,在
分,在 处每投进一球得
处每投进一球得 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用 表示,如果
表示,如果 的值不低于
的值不低于 分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在
分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在 处投一球,以后都在
处投一球,以后都在 处投;方案2:都在
处投;方案2:都在 处投篮.甲同学在
处投篮.甲同学在 处投篮的命中率为
处投篮的命中率为 ,在
,在 处投篮的命中率为
处投篮的命中率为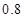 .
.
(Ⅰ)甲同学选择方案1.
求甲同学测试结束后所得总分等于4的概率;
求甲同学测试结束后所得总分 的分布列和数学期望
的分布列和数学期望 ;
;
(Ⅱ)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
在某校组织的一次篮球定点投篮测试中,规定每人最多投 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得 分,在
分,在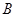 处每投进一球得
处每投进一球得 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用 表示,如果
表示,如果 的值不低于
的值不低于 分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在
分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在 处投一球,以后都在
处投一球,以后都在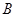 处投;方案2:都在
处投;方案2:都在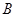 处投篮.甲同学在
处投篮.甲同学在 处投篮的命中率为
处投篮的命中率为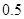 ,在
,在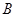 处投篮的命中率为
处投篮的命中率为 .
.
(Ⅰ)甲同学选择方案1.
求甲同学测试结束后所得总分等于4的概率;
求甲同学测试结束后所得总分 的分布列和数学期望
的分布列和数学期望 ;
;
(Ⅱ)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得 分,在
分,在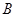 处每投进一球得
处每投进一球得 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用 表示,如果
表示,如果 的值不低于
的值不低于 分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在
分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在 处投一球,以后都在
处投一球,以后都在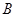 处投;方案2:都在
处投;方案2:都在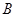 处投篮.甲同学在
处投篮.甲同学在 处投篮的命中率为
处投篮的命中率为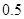 ,在
,在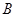 处投篮的命中率为
处投篮的命中率为 .
.(Ⅰ)甲同学选择方案1.
求甲同学测试结束后所得总分等于4的概率;
求甲同学测试结束后所得总分
 的分布列和数学期望
的分布列和数学期望 ;
;(Ⅱ)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
在某校组织的一次篮球定点投篮测试中,规定每人最多投3次.每次投篮的结果相互独立.在A处每投进一球得3分,在B处每投进一球得2分,否则得0分.将学生得分逐次累加并用ξ表示,如果ξ的值不低于3分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在A处投一球,以后都在B处投:方案2:都在B处投篮.甲同学在A处投篮的命中率为0.5,在B处投篮的命中率为0.8.
(1)当甲同学选择方案1时.
①求甲同学测试结束后所得总分等于4的概率:
②求甲同学测试结束后所得总分ξ的分布列和数学期望Eξ;
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看习题详情和答案>>
(1)当甲同学选择方案1时.
①求甲同学测试结束后所得总分等于4的概率:
②求甲同学测试结束后所得总分ξ的分布列和数学期望Eξ;
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看习题详情和答案>>
在某校组织的一次篮球定点投篮测试中,规定每人最多投3次.每次投篮的结果相互独立.在A处每投进一球得3分,在B处每投进一球得2分,否则得0分.将学生得分逐次累加并用ξ表示,如果ξ的值不低于3分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在A处投一球,以后都在B处投:方案2:都在B处投篮.甲同学在A处投篮的命中率为0.5,在B处投篮的命中率为0.8.
(1)当甲同学选择方案1时.
①求甲同学测试结束后所得总分等于4的概率:
②求甲同学测试结束后所得总分ξ的分布列和数学期望Eξ;
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看习题详情和答案>>
(1)当甲同学选择方案1时.
①求甲同学测试结束后所得总分等于4的概率:
②求甲同学测试结束后所得总分ξ的分布列和数学期望Eξ;
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看习题详情和答案>>