摘要：20．已知函数均成立时.求实数a的取值范围.
网址：http://m.1010jiajiao.com/timu3_id_513537[举报]
已知函数 f（x）=
x2-2alnx+（a-2）x，a∈R．
（Ⅰ）当a=1时，求函数f（x）的最小值．
（Ⅱ）当a=-1时，求证：无论c 取何值，直线y=-6
x+c均不可能与函数f（x）相切；
（Ⅲ）是否存在实数a对任意的x1，x2∈（0，+∞）且x1≠x2，有
＞a恒成立，若存在求出a的取值范围，若不存在，说明理由．
查看习题详情和答案>>
| 1 |
| 2 |
（Ⅰ）当a=1时，求函数f（x）的最小值．
（Ⅱ）当a=-1时，求证：无论c 取何值，直线y=-6
| 2 |
（Ⅲ）是否存在实数a对任意的x1，x2∈（0，+∞）且x1≠x2，有
| f(x2)-f(x1) |
| x2-x1 |
已知函数f （x）=ex，g（x）=lnx，h（x）=kx+b．
（1）当b=0时，若对?x∈（0，+∞）均有f （x）≥h（x）≥g（x）成立，求实数k的取值范围；
（2）设h（x）的图象为函数f （x）和g（x）图象的公共切线，切点分别为（x1，f （x1））和（x2，g（x2）），其中x1＞0．
①求证：x1＞1＞x2；
②若当x≥x1时，关于x的不等式ax2-x+xe-x+1≤0恒成立，求实数a的取值范围．
查看习题详情和答案>>
（1）当b=0时，若对?x∈（0，+∞）均有f （x）≥h（x）≥g（x）成立，求实数k的取值范围；
（2）设h（x）的图象为函数f （x）和g（x）图象的公共切线，切点分别为（x1，f （x1））和（x2，g（x2）），其中x1＞0．
①求证：x1＞1＞x2；
②若当x≥x1时，关于x的不等式ax2-x+xe-x+1≤0恒成立，求实数a的取值范围．
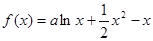
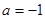时，求函数
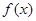的单调区间;
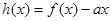，对定义域内任意x,均有
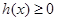恒成立，求实数a的取值范围？
，
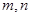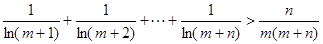恒成立。
的图象关于点（0，1）对称，求实数m的值；
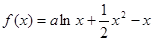
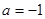时，求函数
的单调区间;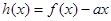
，对定义域内任意x,均有
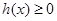恒成立，求实数a的取值范围？
，
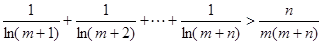恒成立。