(本小题满分12分)已知函数f(x)=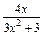,x∈［0，2］.
（1）求f(x)的值域；
（2）设a≠0,函数g(x)=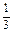ax³-a²x,x∈［0，2］.若对任意x₁∈［0，2］，总存在x₂∈［0，2］，使f(x₁)-g(x₂)=0.求实数a的取值范围.

(本小题满分12分)已知函数f(x)＝x³＋x²－2.

(1)设{a_n}是正数组成的数列，前n项和为S_n，其中a₁＝3.若点(a_n，a_n＋1²－2a_n＋1)(n∈N^*)在函数y＝f′(x)的图象上，求证：点(n，S_n)也在y＝f′(x)的图象上；

(2)求函数f(x)在区间(a－1，a)内的极值．

(本小题满分12分)已知函数f(x)=,x∈［0，2］.

（1）求f(x)的值域；

（2）设a≠0,函数g(x)=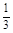ax³-a²x,x∈［0，2］.若对任意x₁∈［0，2］，总存在x₂∈［0，2］，使f(x₁)-g(x₂)=0.求实数a的取值范围.

(本小题满分12分)

已知函数f(x)=2x的定义域是[0,3]，设g(x)=f(2x)-f(x+2).

（1）求g(x)的解析式及定义域;

（2）求函数g(x)的最大值和最小值.

(本小题满分12分)
已知函数f(x)=2x的定义域是[0,3]，设g(x)=f(2x)-f(x+2).
（1）求g(x)的解析式及定义域;
（2）求函数g(x)的最大值和最小值.